Jak się do tego zabrać? Zosia: Funkcja f określona jest wzorem f(x) = x + Ix +1I. Udowodnij, że nie istnieje pochodna funkcji f w punkcie 1.

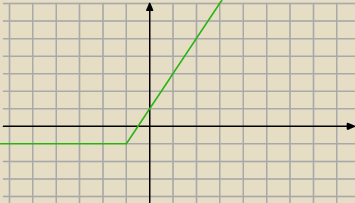
Jerzy: Trudno dowodzić coś, co jest nieprawdą. f(1) = 2

Jerzy: Oczywiście: f'(1) = 2

Zosia: f prim tak? i takie uargumentowanie wystarczy?

Jerzy: Podejrzewam,że w treści jest " nie istnieje w punkcie: −1"

Zosia: nie nie, "że nie istnieje w punkcie 1"

Jerzy: No to istnieje i wynosi 2 : f'(1) = 2

Zosia: przepraszam Pana bardzo kolega źle podyktował zadanie f{x) = x + Ix−1l.

Adamm: zadanie jest bardzo proste

	f(x)−f(1)		f(x)−f(1)
liczysz limx→1−		oraz limx→1+
	x−1		x−1

Zosia: ale jak to obliczyć? kompletnie nie wiem

Adamm: Zosia, no trudno

Jerzy: Rozpisz sobie funkcję dla: x < 1 oraz: dla x ≥ 1

Adamm:

	f(x)−f(1)		x+(1−x)−1
limx→1−		= limx→1−		= 0
	x−1		x−1

	f(x)−f(1)		x+(x−1)−1
limx→1+		= limx→1+		= 2
	x−1		x−1

zatem pochodna nie istnieje w punkcie x=1

Michał: dlaczego w mianowniku jest x − 1?

dream87: no właśnie?

Adamm: proszę o doczytanie tematu zamiast komentarzy i odgrzewania kotletów

Krzysiek: no właśnie?

Adamm: Krzysiek, widzę że pan jest mało inteligentny

Adamm: ah, nieważne przeczytałem w liczniku i myślałem że się o to czepiacie w mianowniku jest x−1 z definicji pochodnej

Adamm: przepraszam za jakiekolwiek nieprzyjemności, myślałem że na mnie naskakujecie