Zad. poziom matury rozszerzonej, okrąg wpisany w trójkąt Jarek: Na okręgu o promieniu 6 cm opisano trójkąt równoramienny o kącie między ramionami 150 stopni. Oblicz długość podstawy tego trójkąta. Proszę o dokładne wytłumaczenie zadania i rozwiązanie go za pomocą wzorów i umiejętności na poziomie matury rozszerzonej z matematyki, gdyż rozwiązanie tego zadania na internecie jest, ale z wykorzystaniem wzoru Herona, a mi to nic nie mówi. Z góry dziękuję.

Bogdan: Korzystając z twierdzenia sinusów otrzymujemy: .... (dokończ)

Mila: Witaj Bogdanie Na okręgu opisano trójkąt .

Bogdan: No tak, chyba się starzeję witaj Mila

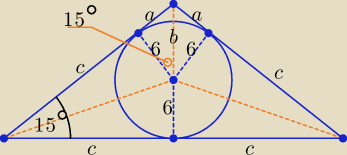
Bogdan: Szkic: Środek okręgu wpisanego to punkt przecięcia dwusiecznych kątów wewnętrznych.

6		6
	= cos15o ⇒ b =
b		cos(45o − 30o)

6 + b		6 + b
	= tg15o ⇒ c =
c		tg(45o − 30o)

Długość podstawy trójkąta jest równa 2c Są inne sposoby rozwiązania zadania

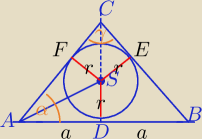
Mila: I sposób r=6 γ=150^o α=(180−150):2=15^o

	α		r
tg		=
	2		a

	6
tg(7.5o)=
	a

obliczyć tg(7.5^o) i będzie rozwiązane. Trochę jest z tym kłopotu. II sposób W ΔCSE:

	r
1) sin(75o)=
	|SC|

sin(75^o)=sin(30+45)= możesz to rozpisać z wzoru sin(α+β)

	1		√2		√3		√2
=sin30*cos45+cos30*sin45=		*		+		*		⇔
	2		2		2		2

	√2+√6
sin(75o)=
	4

==========

√2+√6		6
	=
4		|SC|

⇔|SC|*(√2+√6)=24 |SC|*(√2+√6)=24/*(√6−√2) |SC|*(6−2)=24*(√6−√2) /:4 |SC|=6*(√6−√2) |CD|=h=6*(√6−√2)+6 W ΔCDB:

	a
tg75=
	h

	sin75
a=h*tg75o=h*		, cos75 oblicz podobnie jak sin75
	cos75

a=[6*(√6−√2)+6]*(2+√3)=6*[√6−√2+1]*(2+√3) a=6*(√6+√3+√2+2) |AB|=2a=12*(√6+√3+√2+2) ======================

Bogdan:

	α		1 + cosα
Inny sposób (rysunek ten sam). ctg		=
	2		sinα

c		15		1 + cos15o
	= ctg(		)o =
6		2		sin15o

	1 + cos(45o − 30o)
c = 6 *		= ...
	sin(45o − 30o)

Jarek: Dziękuję Wam oboje za pomoc, jednak bardziej przemówił do mnie sposób Bogdana. I wynik zgadza się z odpowiedziami

Mila: To pięknie.