Granice asymptoty i inne bajery. Sprawdzenie
BiednyStudent:
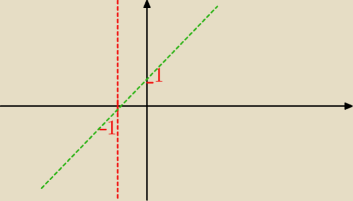
Naszkicuj wykres f: R−> R która jest lewostronnie ciągła w punkcie x
0=2
jej asymptotą poziomą w minus nieskończoności jest y= −1 oraz asymptotą ukośną w plus
nieskończoności
jest prosta y= x+1.
Czy asymptoty są dobrze narysowane?
jeżeli funkcja jest lewostornnie ciągła w pkt x
0=2 tzn że lim
(x−>2
−)= f(2) ale jak to
narysować?
Kurczę nie rozumiem co znaczy "jest asymptotą w +/− nieskończoności"
24 sty 13:30
BiednyStudent:
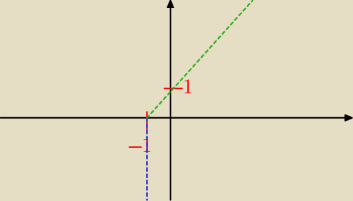
Czy tak? Ale to chyba nie ma sensu prawda?
24 sty 13:32
Jerzy:
Nie ... narysowałeś asymptotę : x = −1
24 sty 13:32
BiednyStudent: o w mordę fakt
24 sty 13:33
Jerzy:
Tzn ,że jak x → +/− ∞ , to wykres funkcji zbliża się do asymptoty.
24 sty 13:34
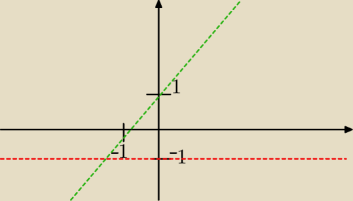
BiednyStudent:
24 sty 13:34
Jerzy:
Teraz dobrze.
24 sty 13:35
BiednyStudent: no okej a jaj narysować tą ciągłość bo to że lim
x−>2−= f(2) nie za wiele mi daje

24 sty 13:39
Jerzy:
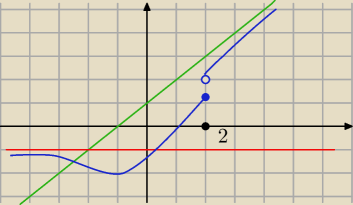
24 sty 13:45
BiednyStudent: no a co z asymtotami? Czy one powinny być "przecięte" wykresem funkcji?
24 sty 13:58
Jerzy:
Funkcja może przecinać asymptotę, aby w nieskończoności tylko się do niej zbliżać.
24 sty 14:01
 Naszkicuj wykres f: R−> R która jest lewostronnie ciągła w punkcie x0=2
jej asymptotą poziomą w minus nieskończoności jest y= −1 oraz asymptotą ukośną w plus
nieskończoności
jest prosta y= x+1.
Czy asymptoty są dobrze narysowane?
jeżeli funkcja jest lewostornnie ciągła w pkt x0=2 tzn że lim(x−>2−)= f(2) ale jak to
narysować?
Kurczę nie rozumiem co znaczy "jest asymptotą w +/− nieskończoności"
Naszkicuj wykres f: R−> R która jest lewostronnie ciągła w punkcie x0=2
jej asymptotą poziomą w minus nieskończoności jest y= −1 oraz asymptotą ukośną w plus
nieskończoności
jest prosta y= x+1.
Czy asymptoty są dobrze narysowane?
jeżeli funkcja jest lewostornnie ciągła w pkt x0=2 tzn że lim(x−>2−)= f(2) ale jak to
narysować?
Kurczę nie rozumiem co znaczy "jest asymptotą w +/− nieskończoności"
 Czy tak? Ale to chyba nie ma sensu prawda?
Czy tak? Ale to chyba nie ma sensu prawda?


