maa mateusz: Sposrod wszystkich wierzcholkow szesciokata o boku dlugosci 1 wybieramy losowo dwa z nich. Oblicz prawdopodobienstwo ze dlugosc odcinka o koncach w wybranych punk tach bedzie wieksza o 1,5

Jerzy: Ile jest takich odcinków ?

kasia: Nwm

Jerzy: No to trzeba policzyć jakie długości mają przekątne.

mateusz: A pomozesz

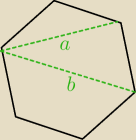
Jerzy: Są tylko takie przekątne : b = 2*a = 2*1 = 2 a − wylicz z trójkąta równoramiennego o ramieniu 1 i kącie rozwartym 120^o

mateusz: I co dalej?

Jerzy:

	6 2
IΩ| =

	n 2
|A| =		( n ilość odcinków spełniających podany warunek )

Maja: IAI=n

Jerzy: A dlaczego n ?

Maryla27: n jest zdarzeniem sprzyjającym.

Jerzy: Nie ... n to ilość odcinków spełniających warunki zadania, czyli ich długość > 1,5

Maryla27: n=6 |A|−zdarzenie sprzyjające

Maryla27: Dziękuję i przepraszam.

Jerzy: Podsumujmy: Wszystkich odcinków jest 15 ( 6 boków + 9 przkątnych ) Odcinki spełniające warunki zadania ( d > 1,5) to tylko przekątne ( n = 9 ) Losujemy dwa odcinki:

	15 2
IΩI =

	9 2
IAI =

	9 2
P(A) =
	15 2

mateusz: Aaaa

Maja: Jerzy, wybieramy dwa punkty, a nie odcinki. stąd IΩI =15, IAI=9.