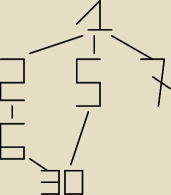
Hassy Opos: Diagram Hassego i jego elementy dla zbioru {1,2,5,6,7,30}. a)wartość maksymalna : 30 wartość minimalna :1 b)element największy :brak element najmniejszy :1 c)łańcuchy antyłańcuchy : (maksymalne) : (maksymalne 1−2−6−30 2−5−7 1−5−30 2−5 1−7 6−5 2−6−30 30−7 5−30 5−7 d)kres górny i dolny podzbioru {2,5,6} kres dolny : 2 kres górny :6 Proszę o sprawdzenie czy wszystko jest w porządku ? Jeżeli coś jest nie tak to proszę o poprawienie oraz sensowne wytłumaczenie.

KKrzysiek: jest ok

KKrzysiek: te łancuchy mi coś nie pasują

KKrzysiek: 1−2−6−20 1−5−7 1−7 tak chyba to powinno wyglądać

Opos: Dlaczego tak ? I w pierwszym chodziło Ci o 1−2−6−30, który został już wymieniony?

Opos: 1−5−7 przecież nie jest łańcuchem

KKrzysiek: Tak , zgadza się, źle popatrzyłem. 1−5−7 nie jest łancuchem. Powinno być 1−5−30. Wydaję mi się, że nie możesz napisać 2−6−30, bo już jest jeden łancuch 1−2−6−30

KKrzysiek: Łancuch chyba jest wtedy kiedy nic powyżej i poniżej nie ma.

Opos: Wydaje mi się, że to nadal jest łańcuch, ale po prostu krótszy. W poleceniu miałem "po przynajmniej 5 maksymalnych łańcuchów oraz antyłańcuchów"

Opos: Całkowicie nie wiem czy kresy są prawidłowo, mam wątpliwości co do tych wartości. Ale chyba trzeba poczekać na jeszcze kogoś, kto byłby w stanie potwierdzić/poprawić.

KKrzysiek: Jest niewiele osób na tym forum , które znają się na tym (to znaczy pamiętają coś z logiki i teorii mnogości).

Opos: Eh, mam jutro kolosa z tego a ni cholery nie mogę załapać tych kresów.

KKrzysiek: "Ograniczenie górne to dowolny element, który jest większy równy od wszystkich elementów w tym zbiorze względem rozpatrywanego porządku, czyli taka, która jest podzielna przez wszystkie elementy tego zbioru, czyli jest ich wspólną wielokrotnością (czyli na pewno nie 200...). Kres górny to najmniejsze z ograniczeń górnych, czyli w tym wypadku najmniejsza wspólna wielokrotność. Ograniczenia dolne i kres dolny − podobnie. " https://www.matematyka.pl/319123.htm

Opos: Czyli kresem dolnym podzbioru {2,5,6} będzie 1, a górnym 30, dobrze rozumiem ?

Opos: Tutaj jeszcze to samo dla zbioru uporządkowanego {{a},{b},{d},{a,c},{a,b,c},{a,b,c,d}}, mógłbyś sprawdzić czy wszystko jest okej ? http://imgur.com/a/licJN

Opos:

Opos:

Opos: ?

olekturbo: nie ma tutaj wartości maksymalnej

Opos: Masz na myśli największej czy maksymalnej ? Maksymalna chyba zawsze jest(?)

KKrzysiek: Błąd, bo posiada element maksymalny. Element ten jest jednocześnie największy.

KKrzysiek: Dobra, źle przeczytałem − już jewt całkiem późno. Zadanie jest dobrze zrobione i diagram Hassego jest dobrze narysowany, ale upewnij się co do tych łańcuchów..