znajdź równanie xyz: znajdź równanie płaszczyzny przechodzącej przez proste : x−3/1=y−1/−1=z+1/−2 i x+1/1=y/−1=z/−2

Mila:

	x−3		y−1		z+1
l1:		=		=
	1		−1		−2

	x+1		y		z
l2:		=		=
	1		−1		−2

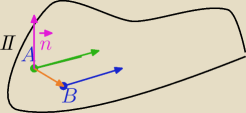
k=^→[1,−1,−2] wektor kierunkowy prostej l₁ i prostej l₂ Proste są równoległe. A=(3,1,−1)∊l₁ B=(−1,0,0)∊l₂ AB^→=[−4,−1,1] n^→=[1,−1,−2] x [−4,−1,1]=[−3,7,−5] wektor normalny płaszczyzny π: −3*(x−3)+7*(y−1)−5*(z+1)=0 π: −3x+7y−5z−3=0