yht:
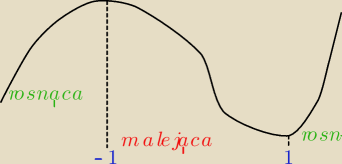
f(x) = x−2arctgx
Dziedzina: x∊R
monotoniczność obliczamy z pierwszej pochodnej:
| | 2 | |
f'(x) = (x−2arctgx)' = 1− |
| |
| | 1+x2 | |
f(x) rosnąca wtedy, gdy f'(x)>0
| | 2 | |
f'(x)>0 wtedy gdy 1− |
| >0 |
| | 1+x2 | |
Uwaga!
Przy mnożeniu i dzieleniu stronami przez liczbę dodatnią znak nierówności nie ulega zmianie, a
przez ujemną − należy go zmienić
musimy mieć pewność że mnożymy nierówność stronami przez liczbę dodatnią
stąd zwyczaj że w celu pozbycia się ułamka mnożymy zwykle przez kwadrat mianownika żeby mieć
pewność że mnożymy przez liczbę dodatnią (bez zmiany znaku nierówności)
tutaj liczba w mianowniku 1+x
2 jest dodatnia dla każdego x∊R
więc (wyjątkowo) można pomnożyć przez mianownik a nie kwadrat mianownika
1(1+x
2)−2>0
1+x
2−2>0
x
2−1>0
(x−1)(x+1)>0
x∊(−
∞,−1), (1,+
∞) − na każdym z tych przedziałów f(x) jest rosnąca
malejąca będzie gdy f'(x) < 0
obliczenia te same tylko znak inny
...
(x−1)(x+1)<0
x∊(−1,1) − wtedy f(x) malejąca
ekstrema:
na podstawie wyliczonej monotoniczności, obserwując wykres, można wysnuć wnioski co do
ekstremów (i ich rodzajów − min czy max):
(−
∞,−1) rosnąca, (−1,1) malejąca, (1,+
∞) rosnąca
Mamy zatem 2 ekstrema:
x = −1 (max)
x = 1 (min).
Przedziały wypukłości z 2−giej pochodnej:
| | 2 | | 4x | |
f''(x) = (1− |
| )' = |
| |
| | 1+x2 | | (1+x2)2 | |
obliczysz ją stosując wzór na pochodną ilorazu
f(x) jest wypukła gdy f''(x)>0
| | 4x | |
f''(x) > 0 wtedy gdy |
| > 0 |
| | (1+x2)2 | |
4x > 0
x > 0
f(x) dla x∊(0,+
∞) jest wypukła
f(x) jest wklęsła gdy f''(x) < 0
4x<0
x < 0
f(x) dla x∊(−
∞, 0) jest wklęsła
f(x) ma punkt przegięcia gdy f''(x)=0
4x = 0
x = 0 − punkt przegięcia
asymptoty ukośne:
asymptota ukośna lewostronna:
y = a
1x+b
1
gdzie:
| | f(x) | |
jeśli granica limx→ −∞ |
| wyjdzie 0, −∞, +∞, to w tych trzech przypadkach asymptota |
| | x | |
ukośna lewostronna nie istnieje!
| | f(x) | | x−2arctgx | | 2arctgx | |
limx→ −∞ |
| = limx→ −∞ |
| = limx→ −∞ 1 − |
| = |
| | x | | x | | x | |
| | −π/2 | | π | |
1−2* |
| = 1+ |
| = 1−0 = 1 − czyli asymptota ukośna lewostronna istnieje |
| | −∞ | | −∞ | |
b
1 = lim
x→ −∞ f(x) − a
1*x = lim
x→ −∞ x−2arctgx −1*x = lim
x→ −∞ x−2arctgx−x = lim
x→
| | π | |
−∞−2arctgx = −2*(− |
| ) = π |
| | 2 | |
y = x+π − równanie asymptoty ukośnej lewostronnej
−−−
asymptota ukośna prawostronna
y = a2x+b2
gdzie
tak samo, jeśli ta granica wyniesie 0, +∞ bądź −∞, to asymptota ukośna prawostronna nie
istnieje
| | f(x) | | x−2arctgx | | 2arctgx | | 2*π/2 | |
limx→∞ |
| = limx→∞ |
| = limx→∞ 1− |
| = 1− |
| = |
| | x | | x | | x | | +∞ | |
1−0 = 1
| | π | |
b2 = limx→∞ f(x) − a2*x = limx→∞ x−2arctgx−1x = limx→∞ −2arctgx = −2* |
| = −π |
| | 2 | |
a2 = 1, b2 = −π
y = x−π − równanie asymptoty ukośnej prawostronnej
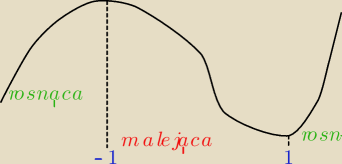 f(x) = x−2arctgx
Dziedzina: x∊R
monotoniczność obliczamy z pierwszej pochodnej:
f(x) = x−2arctgx
Dziedzina: x∊R
monotoniczność obliczamy z pierwszej pochodnej: