Dziękuję za wyrozumiałość :) Cynamonek: tgx = ¹₅ i x jest kątem ostrym oblicz ^cosx_{sin² x} wiem, że ctgx= 5 czyli ^ctgx_sinx zostaje mi? co dalej? dziękuję za pomoc 5−latek ale nie do końca rozumiem co dalej mam zrobić sinx − cosx = ^{5 − 2 √6}₇ i tgx= ^5√6₁₂ 2cosx −3sinx wiedząc, że ctg=2cosx i x należy (0⁰ ; 90⁰) tgx=¹₅ − 3* (√1− cos²x) ? dobrze kombinuję?

azeta: można tez w ten sposób:

	1
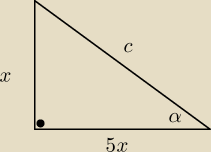
zmieniłem oznaczenia u mnie alfa to kąt, a x to jakaś liczba rzeczywista dodatnia − tgα=
	5

dla α∊(0,90) reprezentuje pewną "rodzinę" trójkątów o cechach jak na rysunku: x²+(5x²)=c² 26x²=c² c=x√26

	x		√26
zatem sinα=		=
	x√26		26

	5x		5√26
a cosα=		=
	x√26		26

inny sposób:

	sinx		1		1
tgx=		=		=> sinx=		cosx => jedynka trygonometryczna sin2x+cos2x=1
	cosx		5		5

1
	cos2x+cos2x=1
25

26
	cos2x=1
25

	25
cos2x=
	26

	5		5√26
cosx=		=		(pamiętając że dla kątów (0,90) − sinx>0 i cosx>0
	√26		26

Cynamonek: Super rozwiązane dziękuję bardzo Tak szeroko i zrozumiałego materiału jeszcze nie miałem ! Dziękuję super! Czy mógłbym prosić o rozwiązanie reszty przykładów?