Obliczyć pole obszaru ograniczonego krzywymi Michał: Obliczyć pole obszaru ograniczonego krzywymi: y = x−2 oraz y²=x ∫ x^1/2 −(x−2) ograniczona od 0 do 4 => ²₃x^3/2−¹₂x²+2x | od 0 do 4 ²₃*4^3/2−¹₂*4²+2*4= ... Czy ktoś może sprawdzić czy rozwiązałem do zadanie poprawnie? A jeśli są jakieś błędy prosiłbym o wskazówkę do rozwiązania.

Michał: @ UP

piotr: ∫−12 ∫y2y+2 dx dy = ∫−12 (−y2+y+2) dy = 9/2

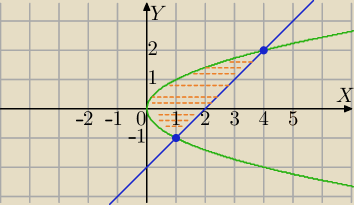Mila: y=x−2 i y²=x⇔ x=y+2 i x=y² obszar jest normalny względem osi OY Punkty przecięcia : (1,−1) i (4,2)

	1		1
P=−1∫2(y+2−y2) dy=[		y2+2y−		y3]−12=
	2		3

Mila: =4.5