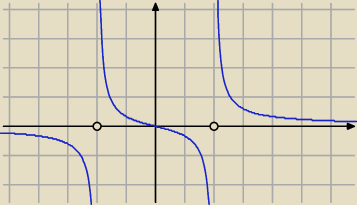
przebieg zmienności funkcji starcie: Zbadaj przebieg zmienności funkcji f(x)= x/(x²−4) Proszę o pomoc,bo wychodzą mi wysokie potęgi i nie wiem co z nimi zrobić

Jerzy: A gdzie masz takie wysokie potęgi ?

5-latek: Witaj No beda np przy 1 pochodnej w mianowniku (x²−4)²

Jerzy: Cześć ... ale akurat w przypadku mianownika pochodnej interesuje nas tylko jego znak

Janek191: x ≠ −2 i x ≠ 2

	x
f(x) =
	x2 −4

	x2 − 4 − x*2x		− x2 − 4
f '(x) =		=		< 0 dla x ∊ Df
	(x2 − 4)2		(x2 − 4)2

więc f maleje w swojej dziedzinie. Oblicz granice w −∞ i w +∞ oraz granice jednostronne.

Jerzy: Jak widać Jankowi wysokie potęgi nie przeszkadzały

5-latek: Witaj Janek191

starcie: Akurat z pierwszą pochodną sobie poradziłem problem mam z drugą,bo mam tam nawet x⁷

Janek191: Witaj Małolatku

Janek191: Do czego potrzebna f '' ? Do punktu przegięcia ?

starcie: tak

starcie: pomoże ktoś?

5-latek: f(x)= −x²−4 f'(x)= −2x g(x)= (x²−4)²= x⁴−8x²+16 g'(x)= 4x³−16x

	f		−2x(x4−8x2+16)−(−x2−4)(4x3−16x)
(		)''=		=
	g		[(x2−4)2]2

	2x5+16x3−96x
	[(x−4)2]2

5-latek: 2x⁵+16x³−96x=0 x(2x⁴+16x²−96)=0 ⇒x=0 lub 2x⁴+16x²−96=0 2x⁴+16x²−96=0 Δ= b²−4*a*c= 16²−4*2*(−96)= 1024⇒√1024= 32

	−b−√Δ		−16−32
x12=		=		= −12 (odpoda
	2a		4

	−b+√Δ		−16+32
x22=		=		= 4 ⇒x2= 2 lub x2=−2
	2a		4