układ nierównośći
kama: Rozwiąż układ nierówności
| 2x+15 | | 1 | | x | |
| > |
| (x−1)+ |
| tu pomnożyłam pzrez 45 |
| 9 | | 5 | | 3 | |
stad otrzymałam
ale odpowiedzi sie niestety nie zgadzaja
22 sty 12:02
===:
... czy na pewno możesz tak pomnożyć drugą nierówność

22 sty 12:06
kama: nie bo dziedzina x≠0
czyli w drugiej nierówności bedzie
| 1 | |
| <0 i tu powinnam narysowac wykres i odczytac tak? |
| x | |
22 sty 12:12
===:
chcieć ... to móc

22 sty 12:14
===:
bez wykresu też sobie poradzisz

22 sty 12:15
kama: no wlasnie nie bardzo wiem, bo w pierwszym zaznaczam na osi
−x+6>0
x<6
z drugiego (−∞,0) i rozwiązaniem jest część wspołna tak?
22 sty 12:19
===:
skoro układ ... to część wspólna

22 sty 12:22
kama: a co robimy w układzie gdy w mianowniku jest funkcja kwadratowa,
sprowadzamy do postaci iloczynowej
potem wspólny mianownik
i teraz kurcze jak się pozbyć mianownika mnożymy przez ....
czyli na przykladzie mam taki układ:
2x−1<5
x<8
| 1 | | 1 | |
| − |
| >0 |
| (x+3)(x−5) | | (x+1)(x−2) | |
po odjęciu wyszło mi
x<8
| x+13 | |
| >0 i teraz mam to wszystko pomnożyć przez mianownik ? Podnieść go |
| (x+3)(x−5)(x+1)(x−2) | |
do kwadratu zeby znak się nie zmienił ?
22 sty 12:32
Jerzy:
⇔ (x+13)(x+3)(x−5)(x+1)(x−2) > 0
22 sty 12:33
kama: na marginesie ===: dziękuję za pomoc przy pierwszym,
będę wdzięczna jakbyś mógł pomoc co dalej z tym mianownikiem patrzyłam tu jak to Kuba wyjaśnia,
ale takiego przykladu nie ma

22 sty 12:33
kama: ok tak zrobiłam i część wspołna prawda ?, ale teraz juz z licznika co mi wyjdzie x
2 i zmienną
pomocniczą czy zwyczajnie rozpatrywac typu
x+13>0
x>−13
potem x+3>0
x>−3 itd

?
22 sty 12:35
kama: sorry pomyliłam się x5 i jaką wielomianową wykreślić tak ?
22 sty 12:36
Jerzy:
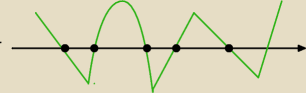
Czrne punkty to miejsca zerowe.
Teraz odczytuj gdziw wielomian jest dodatni.
22 sty 12:51
Jerzy:
Zły rysunek ... poprawię.
22 sty 12:51
Jerzy:
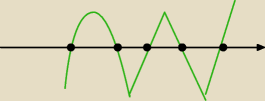
22 sty 12:52
kama: wymnożyć i narysować (x+13)(x+3)(x−5)(x+1)(x−2) > 0 ? to będzie x5 a to wielomian
czy zwyczajnie obliczyć część wspólną dla:
x>.−13
x>−3
x>5
x>−1
x>2 moje ostatnie kombinowanie wydaje mi się głupie
22 sty 12:53
kama: dzięki Jerzy tak myślałam ze wielomian trzeba zrobić dziękuję

22 sty 12:54





 ?
?
 Czrne punkty to miejsca zerowe.
Teraz odczytuj gdziw wielomian jest dodatni.
Czrne punkty to miejsca zerowe.
Teraz odczytuj gdziw wielomian jest dodatni.

