wzór na styczną do wykresu Bravo: Znajdź wzór na styczną do wykresu funkcji we wskazanym punkcie: f(x)=√e^x+3 x0=0

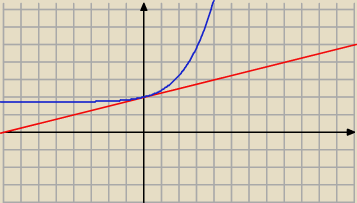
Metis: Styczna to prosta y=ax+b Gdzie z geo. interpretacji pochodnej wiemy, że a=f'(x₀), gdzie x₀ to pkt. styczności. Liczymy wiec pochodną naszej funkcji pierwotnej f(x). f'(x)=(√e^x+3)'

	ex
f'(x)=
	2*√ex+3

	1
f'(0)=		− sprawdź!
	4

	1
Nasz współczynnik kierunkowy stycznej wynosi		.
	4

	1
y=		x+b
	4

Obliczymy teraz współczynnik b. Potrzebujemy do tego punktu. Policzymy f(0) f(0)=2 Nasz punkt to (0,2) − wstawiamy do równania stycznej i liczymy b.

1
	*0+b=2 ⇔ b=2
4

Rówanie szukanej stycznej:

	1
y=		x+2
	4

Adamm:

Bravo: Dziękuję chciałem sprawdzić czy dobrze mi wyszło