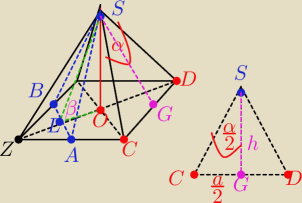
tangens Przyszly_Makler: W ostrosłupie prawidłowym czworokątnym kąt ściany bocznej przy wierzchołku ostrosłupa ma miarę alfa, oblicz tangens kąta, jaki tworzy z płaszczyzną podstawy płaszczyzna przechodząca przez wierzchołek ostrosłupa oraz środki dwóch sąsiednich boków podstawy. Oznaczam bok podstawy jako− a, wysokość ostrosłupa H, wysokość ściany bocznej h.

	a
Trójkąt ZAB jest trójkątem prostokątnym równoramiennym o bokach |ZA|=|ZB|=		i |AB|=
	2

	a√2
	2

	a√2
Więc odcinek |ZL| z oczywistych własności to		.
	4

	a√2
|LO| = U{a{√2}{2} − |ZL| =
	4

	SO		H
Przyda nam się to do liczenia pożniejszego tgβ, bo to		=
	LO		a√2   4

Z trójkąta równoramiennego SCD mamy trójkąt prostokątny SGC.

	α		a   2
tg		=
	2		h

	a
h=
	α   2tg   2

Z pitagorasa w trójkącie OGS liczę H.

	a		a
H2= (		)2 − (		)2
	α   2tg   2		2

	α   a2(1−tg2 )   2
H2 =
	α   4tg2   2

	α   a√1−tg2   2
H=
	α   2tg   2

	H		α   2(√1−tg2 )   2
tgβ=		=
	a√2   4		α   tg *√2   2

I nawet jak usuwam niewymierność to jest źle.. Nie wiem co gdzie robie, liczę to zadanie już

	α   √2√1+tg2   2
chyba 5x. Wynik z odpowiedzi to:
	α   tg   2

Przyszly_Makler: F5

Ajtek: Źle usuwasz niewymierność na samym końcu.

Przyszly_Makler: Oni maja w odpowiedzi + a ja minus. Zechcesz mi rozpisac jak do tego dojść, proszę ?

Ajtek: Ja błędu nie widzę.

Przyszly_Makler: Czyli błąd w książce, tak ? I czy da się z tej postaci jakoś jeszcze uprościć?

Ajtek: Zostaw tak jak jest. Jak widzisz w książce też wynik jest zapisany podobnie.

Przyszly_Makler: Ok, dzieki.. liczę 5x to samo i wychodzi mi ciągle ten wynik i zapisanie na matematycepisz tego też ciężko to idzie, a tu błąd w książce XD Dziękuję Ajtek'u, że chciało Ci się sprawdzać ; )

Ajtek: Nie ma sprawy, też 3 razy sprawdzałem sposób rozwiązania i błędu nie widzę.

Przyszly_Makler: Super, dziękuję