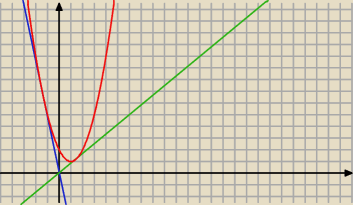
Znajdź równanie prostej stycznej do paraboli. Oliwka: Witam serdecznie, robiłam na lekcji zadania z próbnej matury z tego roku, jednak ani ja, ani nauczycielka nie poradziłyśmy sobie z zadaniem poniższym. Pomocy, błagam! "Prosta przechodząca przez początek układu współrzędnych ma jeden punkt wspólny z parabolą y=(x−1)²+1. Znajdź równanie tej prostej." Ogólnie radzę sobie z parabolą itself, potrafię narysować wyraźny, dobrze opisany wykres, gorzej z wyznaczeniem równania prostej. Nie mam pojęcia z której strony to ugryźć, wyznaczałam już Δ i Δ', nie mam pomysłu co dalej, bo przecież chcę wyliczyć prostą, a nie kolejną parabolę. Z góry dziękuję za pomoc. ;−;

olo: Pierwsza metoda Prosta musi mieć postać y=mx, bo przechodzi przez punkt (0,0), m − parametr A teraz rozwiąż układ równań: y=mx y=(x−1)2+1 Gdy pojawi się równanie kwadratowe, to musi być spełniony warunek Δ=0. Wyjdą dwa rozwiązania − jedna prosta rosnąca, druga malejąca. −−−−−−−−−−−−−−−−−−−−−−−−−−−− Druga metoda − to zastosowanie pochodnej, ale sądzę z zadanego pytania, że jej nie znasz, więc nie opisuję jej.

Adamm: y=ax (x−1)²+1=ax x²+(−2−a)+2=0 Δ=a²+4a−4=0 a=−2+2√2 lub a=−2−2√2

olo: Chochlik Oczywiście drugie równanie y=(x−1)²+1

Oliwka: Nie, pochodnych nie miałam. Bardzo dzięki za pomoc, okazuje się, że dobrze wyliczałam, w takim razie, tylko nie potrafiłam stwierdzić, gdzie jest koniec odpowiedzi. :') Wychodziło mi dobrze do momentu Δ=a²+4a−4=0, tylko do tej pory nie rozumiem czemu pani chciała jeszcze od tego wyliczać Δ' (która notabene wychodzi 32). Już sobie porównam z moimi obliczeniami i zobaczę czy dam radę sama wyliczyć a₁ i a₂, jeszcze raz dzięki.

Oliwka: Okej, dobra, już wiem co i jak w 100%, doszłam jak rozwiązać dzięki końcowym a₁ i a₂! Dzięki bardzo jeszcze raz, ratujesz mi zadek.

Jolanta: musi byc policzona Δ' =32 √32=4√2 i liczysz a₁=−2√2 a₂=−2+2√2

zdziwiony: Do jakiej szkoły chodzisz skoro nauczycielka nie potrafiła rozwiązać zadania − brak kompetencji nauczyciela Poza tym, nie znasz pochodnych? Sądząc z zadania poziom rozszerzony,a na maturze to obowiązek znać pochodne. Nigdy nie było to nauczyciel nie uczył?