[x]/x ciaglosc, rozniczkowalnosc Arius:

	[x]
Witam, prosze o pomoc z f(x)=		. Mam zbadac jej ciaglosc i sprawdzic czy istnieje takie
	x

x0 w ktorym jest rozniczkowalna Zaczalem tak x=/=0 lim x→0+ f(x)=0 lim x→0− f(x)=+∞ wiec nie jest ciagla Dobrze to jest? I jak sprawdzic czy jest rozniczkowalna? Pozdrawiam

Adamm: jeśli [] to cecha, to ona ma nieskończenie wiele punktów dla których nie jest ciągła (co pociąga za sobą że ma nieskończenie wiele punktów dla których nie jest różniczkowalna)

Arius: tak [] to cecha, w jaki sposob powinienem wykazac ze nie jest ciagla w zadnym x0?

Adamm: kto powiedział że w żadnym ? weź 1/2, w tym punkcie jest ciągła oraz różniczkowalna

Arius: ok, zle zinterpretowalem twoja wiadomosc. No to moge sobie strzelac np. z ta 1/2 ale jak formalnie to zapisac, tak zeby z tego mi wyszla np ta 1/2 czy tam inne punkty. Nie wiem czy wiesz o co mi chodzi.

Adamm: zastanów się nad funkcją [x] i od czego zależą jej wartości

Mila: 1) Najpierw narysuj wykres tej funkcji. 2) Prowadź rozważania w punktach nieciągłości: x∊C a potem w przedziałach.

Adamm: raczej x∊ℤ

Arius: wiec f(x)= dla x∊C =1 dla x∊(−∞;0)\{k} ,k∊C ma wartosci z przedzialu (1,2) dla x∊(0;+∞)\{k} ,k∊C ma wartosci z przedzialu <0,1)

Arius: błąd... ok rysuje

Arius: Hmm jak mogę prowadzić rozważania. Wystarczy napisać, że z rysunku wynika, że dla x∊C funkcja nie jest ciągła, więc nie jest też różniczkowalna? I jak zbadać dla przedziałów?

Mila:

	[x]
f(x)=
	x

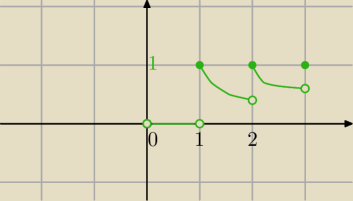
D=R\{0} a)x∊(0,1) to [x]=0 ⇔f(x)=0 b) x∊<1,2)

	[1]
f(1)=		=1
	1

	[x]		1
f(x)=		=
	x		x

	1		2
f(3/2}=		=		,
	3/2		3

	1		5
f(9/5)=		=
	9/5		9

to taki przybliżony szkic z prawej wartości dążą do 1, z lewej zbadaj 2) dla x<0 narysuj dla x∊(−1,0) (ciekawe wartości) i jeszcze dla 2 przedziałów tu sie unormuje jak z prawej.

Mila: Znajdź program do rysowania wykresów . wpisz : (floor(x))/x