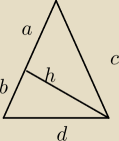Wysokość w trojkącie równoramiennym dzieli pole w stosunku 2:3 oblicz tg SEKS INSTRUKTOR : Wysokość trójkąta równoramiennego dzieli jego pole w stosunku 2:3. Oblicz tg kata przy podstawie. tgα=h/b a*h*1/2 *2 = b*h*1/2*3 a*h=b*h*3/2 a=3/2b 3/2b² +h² = (5/2b)² 6/4b² +h² = 25/4*b² h² = (19b²)/4 h=√19/2 b tgα= √19/2*b/b = √19/2 W odpowiedziach jest wynik 2 lub √21/3, proszę o podpowiedź co robię źle

Mila:

	3		5
(		b)2+h2=(		b)2
	2		2

	16
h2=		b2
	4

h=2b

	2b
tgα=		=2
	b

lub inny podział. Zaraz podam prostszy zapis.

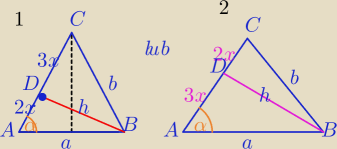Mila: 1)

PΔADB		2
	=		⇔|AD|=2x i |DC|=3x gdzie : x− wspólna miara
PΔCDB		3

W ΔCDB: b=5x (3x)²+h²=(5x)² h=4x

	h		4x
tgα=		=
	|AD|		2x

tgα=2 lub 2) W ΔCDB: h²+(2x)²=(5x)² h²=21x² h=x√21

	x√21
tgα=
	3x

	√21
tgα=
	3

SEKS INSTRUKTOR : Dziękuję, już drugi raz dziś pomagasz! POZDRAWIAM SEKS INSTRUKTOR

Mila: