Analityczna Ja: Znaleźć równanie płaszczyzny przechodzącej przez punkt M(3,1,−2) i prostą

	x−4		y+3		z
		=		=
	5		2		1

jc: Prosta przechodzi przez punkt (4,−3,−1) i ma kierunek (5,2,1). Szukana płaszczyzna wyznaczona będzie przez wektor kierunkowy prostej (5,2,1) i wektor (3,1,−2)−(4,−3,−1) = (−1,4,−1). (3,−2,5) wektor prostopadły do wektorów (−1,4,−1), (5,2,1). Równanie szukanej płaszczyzny: 3(x−4) −2(y+3) + 5(z+1)=0.

jc: Pomyłka. Prosta przechodzi przez punkt (4,−3,0) i ma kierunek (5,2,1). Szukana płaszczyzna wyznaczona będzie przez wektor kierunkowy prostej (5,2,1) i wektor (3,1,−2)−(4,−3,0) = (−1,4,−2). (a,b,c) wektor prostopadły do wektorów (−1,4,−2), (5,2,1). Sam znajdź (ab,c) = (−1,4,−2) x (5,2,1). Równanie szukanej płaszczyzny: a(x−4) +b(y+3) + c(z+1)=0.

Ja: (3,1,−2)−(4,−3,0), w tym miejscu chyba powinno być mnożenie tych wektorów (3,1,−2)x(4,−3,0)

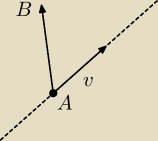
jc: B−A=(3,1,−2)−(4,−3,0) to jest wektor łączący dwa punkty płaszczyzny. v=(5,2,1)

Jerzy: Wektor normalny szukanej płaszczyzny: n^→ = [5,2,1]X[1,−4,2] = [8,−9,−22] Szukana płaszczyzna: 8(x − 3) −9(y − 1) −22(z + 2) = 0