Dwa kąty ostre trójkąta mają miary alfa i beta. oblicz stosunek Adix422: Dwa kąty ostre trójkąta mają miarę α i β. Oblicz stosunek pola tego trójkąta do pola koła opisanego na tym trójkącie. Rozumiem, że trzeba użyć twierdzenia sinusów, albo po wyliczeniu R nie wiem co robić.

Mila:

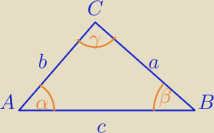
	a		b		c
1)		=		=		=2R
	sinα		sinβ		sin[180−(α+β)]

⇔ a=2R*sinα b=2R sinβ c=2R*sin(α+β) 2)

	1		1
PΔ=		*a*c*sinβ=		*2R*sinα*2R*sin(α+β)*sinβ⇔
	2		2

P_Δ=2R²*sinα*sinβ*sin(α+β) 3)

PΔ		2R2*sinα*sinβ*sin(α+β)
	=		=
Po		πR2

	2
=		*sinα*sinβ*sin(α+β)
	π