part2 Pełcio: #Zakładam nowy wątek. Zapraszam

Metis: Od razu lepiej

Eta:

Pełcio: Na początek wątku pozdrawiamy Etke.

Eta: Hej Metis w piątek będę pozdrawiać Twoje rodzinne miasto

Eta: Witam Pełcio (Pawełku

Metis: Zazdroszczę Etuś Muszę odwiedzić mojego matematycznego profesora w mojej szkole,ale to juz w lutym

Pełcio: Tak właśnie mi na imię, Pełcio to przezwisko z podstawówki Jakby ktoś miał na stanie podobne zadanko do zadania 5 z tamtąd http://www.diament.agh.edu.pl/images/dokumenty/matematyka_I_2016-2017.pdf to chętnie przygarnę

Jack: Pełcio maturzysta?

Metis: Rozwiązywałem kiedyś te zadania − to były czasy

Metis: Mam jeszcze zdjęcia mojej pracy, którą wysyłałem http://image.prntscr.com/image/b7e095bfc4884b2aac69ca8d907ca111.png

Pełcio: Jack, jeszcze na szczęście nie Metis, no te przynajmniej są dla ludzi, nie mam kompletnie motywacji, żeby się wziąć za OMa, za mało cierpliwości mam do tamtych zadań

Pełcio: Tak z ciekawości, jest tutaj ktoś kto przeszedł II etap OM? Niech się zgłosi mistrz

Mila: 1) Rozwiąż równanie:

	1
log√x2+x−5=2logx+log(		)
	x

2) 3^{log₂(x2−5x+7)}=1

Pełcio: Dziękuję Milu! Będę próbował

Ajtek: A co tu się dzieje Witam Obecnych .

Pełcio: 1) x=−3 ∨ x=2 tak mi wyszło, ale mała szansa, że to dobrze

Mila: "Ucho Jakuba".

Pełcio: Powitać, Ajtek.

Mila: Pełcio A dziedzina ? Wpis o kabarecie to do Ajtka.

Pełcio: 1) oczywiście −3 nie może być, to już sobie przegapiłem przedtem

Mila: Dobranoc

Ajtek: Mila, witaj. Załapałem o co chodzi . Pelcio, czy to rozwiązanie do zadanka Mili

Pełcio: Dobranoc

Ajtek: To dobrej nocki Mila .

Metis: Dobranoc Milu

Pełcio: Tak, wyszło mi x=2. Ale moje doświadczenie w równościach i nierównościach logarytmicznych jest... zerowe

Ajtek: Pelcio, najważniejsze w równaniach i nierównościach logarytmicznych jest definicja logarytmu. Czytaj wyznaczenie dziedziny To musisz zrobic na samym początku

relaa: Mam takie malutkie zadanka na rozgrzewkę.

	3
Wyznacz wartość wyrażenia sin(x)cos(x), jeżeli sin(x) + cos(x) =		.
	2

Znajdź takie wartości parametru m dla których równanie sin(3x) = msin(x) ma rozwiązanie.

Ajtek: relaa przyjemne zadanka .

Benny: 1) źle! popraw się

Pełcio: O jest i relaa. I znowu z czymś nowym Jak starczy czasu i sił to coś dziś ruszę, a jak nie to będzie to rozgrzewka jutro Benny myślę, myślę

Ajtek: Uciekam, spokojnej Wszystkim

relaa: Ajtek mam nadzieję, że będą przyjemne. Chcę zobaczyć jak to u Pełcio z myśleniem jest. Rzeczywiście może za bardzo Cię męczę, więc nowych zadań już nie będę wrzucał. Dobranoc Ajtek i ja też będę powoli się zbierał.

Benny: To ja zostanę

Metis: Przede mną nocka z głowy więc też

Pełcio:

	3
sinx+cosx=
	2

	3
cosx=		− sinx
	2

cos²x+ sin²x= 1

	3
(		− sinx)2+ sin2x= 1
	2

9
	− 3sinx+ sin2x= 1
4

	5
sin2x− 3sinx+		= 0
	4

4sin²x− 12sinx+ 5= 0, teraz np. sinx= t 4t²− 12t+ 5= 0 Δ= 64

	1
t1=		to ok
	2

	5
t2=		to nie ok
	2

dobra, tyle na dziś, relaa jak to? to co ja będę robił?

Metis: Rozpisz sobie: (sinx+cosx)² =

Alky: Zapomniałeś o jednym sin²x przy wyliczaniu z jedynki Choć generalnie to najprościej, bo w 2 linijkach możn to zrobić wychodząc z danego równania jak napisał Metis

KKrzysiek: Widzę, że się nudzicie , pewnie macie jutro wolne od zajęć.

Alky: Ja prowadzę nocny tryb życia Za 3 tyg mam kolokwium z analizy na które generalnie wczoraj zacząłem się uczyć(studium talent PWr), a dziś rano przypomniało mi się że za ok 3 miesiace ( + pare dni ) mam tę no... Mature .. Więc uznałem, że może warto się troche pouczyć kapa

Metis: Ja mam jutro dwa kolokwia Alky studium talent masz z dr Żakiem?

KKrzysiek: Ucząc się do matury uczysz się jednocześnie do tego kolokwium. Nie powinno ono być specjalnie trudne skoro jesteś jeszcze w liceum. Także spokojnie się wyrobisz, no ja uczę się na metody numeryczne (na dziś), także trochę jeszcze posiedzę...

KKrzysiek: Przyznam szczerze, że nie za bardzo wiem co to jest studium talent i dla kogo to jest organizowane.

Metis: Studium Talent to specjalny program dla uczniów liceum org. przez Politechniką Wrocławską. Uzyskanie dyplomu to dodatkowe pkt. przy rekrutacji.

KKrzysiek: Jest jakaś selekcja do studium talent?

Metis: Nie mam pojęcia Krzysiek, ale to program przeznaczony tylko dla uczniów wrocławskich liceów.

KKrzysiek: A to tylko dla liceów, i to na dodatek Wrocławskich, raczej by mnie nie chcieli tam.

Metis:

Alky: Studium Talent działa na zasadzie cotygodniowych wykładów z danego zakresu ( np rok temu byłem na Liczbach zespolonych, permutacjach , grupach i czymś tam jeszcze, a w tym roku mam tylko analize, co w sumie nie wydaje się być poki co jakieś ciężkie((Tutaj też odnosząc się do tego co pytałeś Metis, mam z Górniakiem. Rok temu miałem z Kwasnickim, ale ugrałem tylko 3 bo nie przygotowałem się z grup i dowody mnie zabiły W tym roku niżej niż 5 nie biorę ^^ i po około pół roku ( semestr ) jest kolokwium. Nie ma sprawdzanej obecności etc. Ja np nie chodze na te wykłady, byłem moze na 3−4 bo srednio z dojazdem a i tak więcej tam pieprzenia od rzeczy i niepotrzebnych dygresji niż materiału więc bawię się z e−Trapezem. Tamto tłumaczenie zrozumie nawet głuchy i ślepy gimnazjalista ...

Metis: Moim zdaniem warto było dojeżdzać prof. Górniak to świetny matematyk i wykładowca

Alky: @Metis nie tylko wrocławskich i nie tylko licealistó, choć powyżej liceum juz nie ma profitu z tego a przed liceum raczej nikt nie chodzi bo nie mają podstaw albo zwyczajnie nie wiedząjeszcze gdzie chcą iść i czy potrzebują tych punktó ( za odpowiednią ocenę sa dodatkowe punkty + 5 i 6 daje automatyczne wejście na wszystkie kierunki z wydziałów Matematyki i Podstawowych Problemów Techinki ( ja akurat na Informatykę i Zarządzanie więc to tylko punkty ) Rok temu na gratulacjach dla osób z 6 było wyczytane wiele osób z poza Wrocławia

Metis: Możliwe

KKrzysiek: @Alky, nie zgodzę się z Tobą. Uważam , że warto chodzić na wykłady. Czasem mogą się okazać nudne, ale po godzinnym wykładzie jakiś obraz/pogląd się powoli kształtuje w Twojej głowie na dany temat. Mniej−więcej masz jakiś zarys tematu, i jest szansa , że poświęcisz mniej czasu na ogarnianie tego działu samemu, w domu.

Alky: Wiesz, nie mówię że nie, ale mam generalnie problem z dojazdem w weekendy, a prawo jazdy niestety jeszcze in progress Rok temu nie opuściłem ani 1 wykładów bo temat był jak na moje trudny i było mnóstwo dowodów więc notowałem i słuchałem ładnie A teraz to liczenie całek i pochodnych do zakresu kolokwium ogranicza się do znajmości wzorów używania mózgu ^^ Troszkę praktyki i przykładów i pyknie. Zwłaszcza że wszyskie jego zadania są rok w rok bardzo podobne ( bo co innego może dać ) i mam listy zadań sprzed roku do − lat włącznie więc jak uznam że jestem gotowy to zrobię jeszcze to wszysto w ramach sprawdzenia i myślę że powinno pyknąć

Alky: @KKrzysiek nie mówię, że nie warto ( bo chyba nigdzie tak nie powiedziałem ? Może ? ) Jak tylko mogę to chodzę, ale mam problem tego rodzaju że jestem spoza Wrocłąwia i żeby dojechać muszę wstać o 5na autobus bo innego nie mam ( wykład na 9 ) a potem jeszcze 1,5 h nie mma co ze sobą zrobić. Teraz ze względu na męczący dojazd przeniosłem się do Wrocławia i mam dużo czasu i możliwości więc za tydzień jeszcze pójdę na ten ostatni wykład się sprawdzić jak już ogarnę cały zakres . Tak jak mówię. Rok temu chodziłem na wszsytkie bo nie kumałem zakresu, ale teraz to nie wydaje się na tyle ciężkie żebym sobie z tym nie poradził sam

Metis: Ważne, że działasz! Oby tak dalej

Alky: Byle przed siebie. Zobaczymy jak pójdzie Tymczasem spadam się ogarnąć na jutro i może coś jeszcze powtórze Dobranoc

KKrzysiek: Alky, no i prawidłowo. Ważne, że masz taką możliwość, ja na przykład nie miałem takich programów w mieście jak studium talentu. Mam fajną całkę dla Ciebie do przerobienia ∫cos²xdx.

Adam: sin(3x)=3cos²xsinx−sin³x

Adam: (cosx+i*sinx)ⁿ=cos(nx)+i*sin(nx) jedyne co musisz wiedzieć to że i²=−1 dalej porównujesz część z i oraz bez i przyjmując n=3 i biorąc część z i mamynasz wzór na sin(3x)

Pełcio:

	3
sinx+cosx=		/2
	2

	9
sin2x+2sinxcosx+cos2x=
	4

	5
2sinxcosx=
	4

	5
sinxcosx=
	8

rzeczywiście, tak jest zdecydowanie ładniej

relaa: Pięknie, a teraz spytam jesteś pewny swojej odpowiedzi?

Pełcio: Pewnie nie powinienem, skoro tak pytasz Pomyślmy

relaa: Pomyśl i napisz.

Pełcio: nie ma takiej liczby

relaa: Nie rozumiem za bardzo, co masz na myśli pisząc, że nie ma takiej liczby.

Pełcio:

	5
2sinxcosx= sin(2x) a to nie może być
	4

relaa:

	3
Można było od razu zauważyć, że nie istniej taki kąt x dla którego sin(x) + cos(x) =		.
	2

relaa: To zadanie miało haczyk i nikt go nie zauważył.

Pełcio: no właśnie skoro jedynka trygonometryczna to kwadraty, to tymbardziej bez potęg nie może być więcej niż 1

relaa:

	6
Przykładowo sin(x) + cos(x) =		może być?
	5

Pełcio: może być

relaa:

	6
To czemu napisałeś to o 14 : 02? Przecież		jest większe od 1. Chcę zobaczyć, czy dobrze
	5

myślisz.

Jerzy: sinx + cosx = √2sin(π/4+x)

	6		6
√2sin(π/4+x) =		⇔ sin(π/4+x) =		< 1
	5		5√2

Pełcio: Już się skapnąłem że to co tam napisałem to nieprawda, szybko zmieniam zdanie Po prostu sprawdziłem tak samo i wychodzi

	11
sin(2x)=		, a taki może być.
	25

relaa: Chodzi o to, że |sin(x) + cos(x)| ≤ √2.

Pełcio: a to nie znałem czegoś takiego, dzięki

Adamm: sinx+cosx=√2(sinxcos(π/4)+cosxsin(π/4))=√2sin(x+π/4)

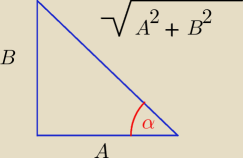
relaa: Można sobie nawet wzór wyprowadzić na zbiór wartości f(x) = Asin(x) + Bcos(x) Asin(x) + Bcos(x) =

	A		B
√A2 + B2[		sin(x) +		cos(x)] =
	√A2 + B2		√A2 + B2

√A² + B²[sin(x)cos(α) + sin(α)cos(x)] = √A² + B²sin(x + α).

Alky: @relaa to że wynik jest sprzeczny można zauważyć po metodzie Pełcia ( tak jak wczoraj liczył obliczając sin potem z tego cos i wynik sin* cos ) bo po poprawieniu i dopisaniu drugiego sin²x wychodzi delta <0 więc nie ma takich sinusów a więc i cosinusów dla których równanie jest spełnione. Liczyłem to 5 razy zeby sprawdzić czy obie metody będą zgodne, ale tą Pełcia nie chciało wyjść więc ostatecznie uznałęm że to ze mną jest coś nie tak i poszedłem spać xD

relaa:

	3
A wystarczyło zobaczyć, że |sin(x) + cos(x)| ≤ √2 <		.
	2

Pełcio: Do zapamiętania

relaa: Masz tam jeszcze inne zadania.

Pełcio: sin(3x) = msin(x) zakładając że to jest prawda sin(3x)= 3cos²xsinx−sin³x 3cos²(x)sin(x)−sin³(x)= msin(x) i teraz nie wiem, bo nie rozwiązywałem takich równań, ale spróbuję tak: 3cos²(x)sin(x)−sin³(x)− msin(x)= 0 sinx(3cos²(x)−sin²(x)−m)=0 tutaj moje możliwości się kończą

relaa: Masz wyznaczyć parametr m dla którego to równanie ma rozwiązanie.

Adamm: pytanie: dla jakich m istnieje rozwiązanie?

Pełcio: no nie wiem, np. 3 − 3sin²x−sin²x=m −4sin²x+3=m

	−m+3
sin2x=
	4

−m+3
	<1
4

m∊(−1,+∞)

Adamm: sinx=0 jest rozwiązaniem niezależnym od m

Pełcio: czyli m∊ℛ ?

relaa: Dokładnie.

Pełcio: Ok, a jeśliby tego sinx z przodu nie było, to to co napisałem byłoby ok?

Adamm: nie, 0≤sin²x≤1

Pełcio: aaa, no tak..

Adamm: zadanie dla ciebie przedstaw sinx, tgx oraz cosx przez tg(x/2)

Adamm: podpowiedź

	1
skorzystaj z tożsamości		=1+tg2(x)
	cos2(x)

Pełcio:

1
	= 1+tg2x
1−sin2x

	1
1−sin2x=
	1+tg2x

	−tg2x
−sin2x=
	1+tg2x

	tg2x
sin2x=		jest sens to ciągnąć czy już gdzieś zrobiłem błąd
	1+tg2x

Adamm: błędu nie zrobiłeś, co prawda nie do końca miałem to na myśli mówiąc by skorzystać z tej tożsamości, ale źle nie jest

Pełcio: czyli

	|tgx|
sinx =
	√1+tg2x

Pełcio: a, ale to miało być tg(x/2)...

Adamm: miałeś to przedstawić przez tg(x/2)

Pełcio: chyba nie dam rady... z trygonometrii to narazie miałem co to tg i ctg i jedynke trygonometryczną, a na połowy kąta muszą być pewnie osobne wzory

Adamm: sin(2x)=2sinxcosx cos(2x)=cos²x−sin²x

Pełcio: no to podwojony sinus już wyżej był, cosinus pierwszy raz widzę

Pełcio: ale to się jakoś ma do połówek?

Benny:

	x   x   2sin cos   2   2
sinx=		teraz próbuj
	x   x   sin2 +cos2   2   2

Adamm:

	1
sinx=2sin(x/2)cos(x/2)=2tg(x/2)
	cos2(x/2)

Adamm:

	1
przepraszam, sinx=2sin(x/2)cos(x/2)=2tg(x/2)
	1   cos2(x/2)

Pełcio: No fajne, fajne.. A teraz mi powiedzcie jak zrobić zadania Mili. Jakie założenia mają być w pierwszym?