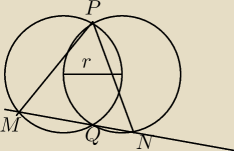
Wykaż że trójkąt MNP jest trójkątem równobocznym Falitac: Okręgi w1 i w2, o jednakowych promieniach, przecinają się w punktach P i Q. Prosta przechodząca przez punkt Q przecina okrąg w1 w punkcie M, a okrąg w2 w punkcie N. Wykazać, że jeśli odległość środków okręgów w1 i w2 jest równa ich promieniowi, to trójkąt MNP jest trójkątem równobocznym.

g: Kąt POQ = 120 (O to środek jednego lub drugiego okręgu). W takim razie katy PMQ i PNQ mają po 60 stopni.

Falitac: Nie rozumiem

Falitac: Z czego to wynika?

Falitac: tzn rozumiem że tam jest 120 stopni ale dlaczego PNQ i PMQ mają 60?

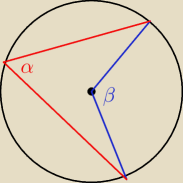
g: α = β/2