dla jakich wartości parametru m równanie ma pierwiastek dodatni ? DominO : dla jakich wartości parametru m równanie ma pierwiastek dodatni ? a) log_0,5(x+4)=^m_m+1 odp to m∊(−1;−²₃) b) 1−3x=log₃m odp to m∊(0;3) c) 3+2x=log_¹3m odp to m∊(0; ¹₂₇)

Adamm: x>0 a) x+4>4 log_0,5(x+4)<log_0,54

m
	<log0,54 (należy założyć m≠−1)
m+1

b) −x<0 1−3x<1 log₃m<1 (oczywiście m>0) c) x>0 3+2x>3 log_1/3m>3 (załóż m>0)

DominO : mógłbyś to jakos bardziej rozpisać ? bo nie rozumiem nadal jak to zrobić i skad takie wyniki...

DominO : haloo pomoże ktoś ?

Jerzy:

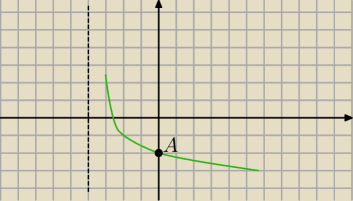
	m
Aby równanie miało pierwiastek dodatni, czerwona prosta y =		musi leżeć
	m+1

poniżej punktu A Punkt A ma rzędną równą: y_A = log_0.54 = −2

	m
Zatem:		< −2 ... i licz.
	m+1

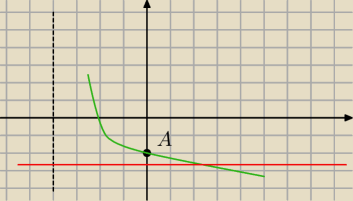
Jerzy: Poprawiałem rysunek i nie narysowałem czerwonej prostej