równania aga: pokazać że nastepujące rownanie ma rozwiązanie: sin x = x−1 w <0, pi>

Jerzy: f(x) = sinx − x + 1 f(0) = 1 f(π) = 1 − π < 0 i twierdzenie Darboux

aga: czyli, możesz dokonczyc albo naprowadzić

Jerzy: Przeczytaj twierdzenie, to sama zrozumiesz

aga: blagam, napisz

Adamm: f'(x)=cos(x)−1≤0 przy czym równość zachodzi jedynie dla x=2πk więc dodatkowo, to jedyne takie rozwiązanie równania dla x∊ℛ

Adamm: https://pl.wikipedia.org/wiki/Twierdzenie_Darboux

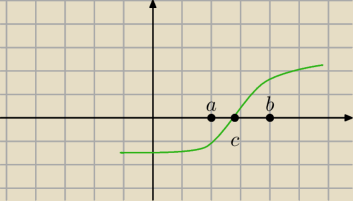
Jerzy: Tu masz ilustrację do twierdzenia: Funkcja jest ciągła w przedziale (a,b) f(a) < 0 i f(b) > 0 W przedziale (a,b) istnieje punkt c taki że, f(c) = 0

aga: ok, już rozumiem