Badanie zmienności funkcji Koala:

	1
1. Zbadać przebieg zmiennosci funkcji f(x)=e/div>		, to jest e do potęgi
	5x−2

Wyznaczyć dziedzinę funkcji; • Wyznaczyć granice(jednostronne) funkcji na końcach określoności dziedziny; • Wyznaczyć asymptoty(Przed obliczeniem “ukośnych” warto też wyznaczyć “poziome”); • Określić przedziały monotoniczności funkcji; • Wyznaczyć przedziały wklesłości i wypukłości funkcji; • Znaleźć ekstrema funkcji; • Znaleźć punkty przegięcia wykresu funkcji; • Naszkicować wykres funkcji.

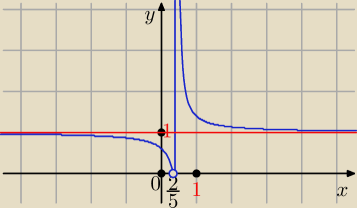
Janek191: f(x) = e^{1_{5 x − 2}} x ≠ ²₅ Df = ℛ \ { ²₅ } lim f(x) = 1 x→−∞ lim f(x) = 1 x→∞ lim f(x) = 0 x→ ²₅⁻ lim f(x) = +∞ x→²₅⁺ Asymptota pozioma : y = 1

	2
Asymptota pionowa: x =
	5

	− 5
f '(x) =		e1 5 x − 2 > 0 dla x ∊ Df
	( 5 x − 2)2

Funkcja f jest malejąca w ( − ∞ , ²₅) oraz w ( ²₅, +∞) Funkcja f jest wklęsła w ( − ∞, ²₅) oraz wypukła w ( ²₅, +∞) f ' się nie zeruje, więc f nie ma ekstremów. Brak punktów przegięcia.

Koala: dziękuje