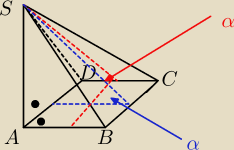
stereo Przyszly_Makler: Bardzo proszę o pomoc, kogoś kto to bardzo dobrze wytłumaczy, bo naprawdę nie jestem w stanie tego pojąć.. Mamy ostrosłup, w którym dwie ściany boczne są prostopadłe do płasczyzny podstawy, a dwie pozostałe ściany boczne tworzą z podstawą kąt α. W podstawie jest kwadrat. Jestem w stanie zrozumieć, że kąty proste są przy wierzchołku A, (choć na początku myślałem, ze powinny być przy wysokościach ścian bocznych, ale wtedy nie powstałby ostrosłup) ale kompletnie nie jestem w stanie zrozumieć, dlaczego CDS i BCS są prostokątne, z czego to wynika? Mógłby ktoś zrozumiale napisać ogólną regułkę, abym mógł lepiej wypatrywać te prostopadłości? Bez zauważnia tego na wstępie jest minus całe zadanie, a z tym darmowe punkty, więc to w sumie ważne... I jeszcze, gdzie jest kąt alfa? Bo mi się wydaje, że powinien być tam, gdzie oznaczyłem na czerwono i niebiesko, a chyba tam nie powinien być.

Przyszly_Makler: przerywana niebieska i czerowna linia to wysokości owych ścian bocznych

Przyszly_Makler: f5

Przyszly_Makler: I skąd wiadomo w tym zadaniu, że wysokość ostrosłupa leży na wysokości podstawy

5-latek: Moze inaczej . Co stoi na przeszkodzie zebys sobie sam zrobil model takiego ostroslupa ? Przeciez jeszce masz czas to zrobic . Potem go nie bedzie

Przyszly_Makler: a na maturze też będę sobie wycinał modele? W matematyce obowiązują pewne twierdzenia, które trzeba opanować i pewne rzeczy "dotrzegać" z marszu. A ja nie wiem jak uzasadnić wątpliwości dot. rys. 1, nic mi nie pasuje, żadne twierdzenie o 3 prostych ani nic.

Mila: Może napisz dokładnie treść zadania, albo podaj linka.

Przyszly_Makler: cd postu o godz: 20:33 chodziło mi− skąd wiadomo w tym zadaniu: https://matematykaszkolna.pl/strona/3669.html że wysokośc ostrosłupa leży na wysokości podstawy. Teraz zauważyłem dopiero, że się nie wkleiło.

5-latek: Kiedys tez mi tak odpisal maturzysta (bo przed matura nie mial czasu ) To jest Twoja broszka co zrobisz

Przyszly_Makler: Mila https://www.zadania.info/d455/1849335

Przyszly_Makler: Akurat 5−latku pracuję bardzo dużo i piszę w ostateczności, cały materiał opanowuję sam, a ponieważ nie chodze do szkoły, naprawdę nie ma kto rozwiać moich pytań.

5-latek: To tak jak ja . Chcialem kupic sobie modele ale zawolali okolo 260 zl Wiec lepiej soboe zrobic

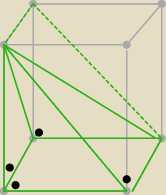
tomek: w tym zadaniu lepiej "dostrzegać to z marszu":

5-latek: Dobry wieczor Milu Dzisiaj juz odpuszczam . Nie wiem jak jutro .

tomek: w opisie rozwiązania prostopadłość wynika z zastosowania tw. o trzech prostych prostopadłych

tomek: Mila z pewnością się wypowie

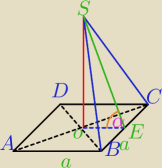
Mila: ABCDS − ostrosłup prawidłowy czworokątny. Na rysunku masz zaznaczony kąt między ścianą boczną ostrosłupa a płaszczyzna podstawy− to jest kąt między wysokością SE a jej rzutem prostokątnym OE na podstawę . Zaraz przejdziemy do Twojego zadania. Tylko inaczej narysujemy ostrosłup, wg mnie bardziej trafiający do wyobraźni.

===: To najsłabiej opisywane w podręcznikach tematy a jeśli już opisywane to nie zawsze w rozdziałach stereometrii czyli troszkę w oderwaniu od brył. Popatrz tu : http://www.interklasa.pl/portal/dokumenty/tab_mat/stereometria/proste.html

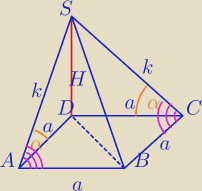
Mila: |AS|=|SC|=√a²+H²− tw. Pitagorasa |SB|²=2a²+H²⇔SB²=BC²+SC²⇔ ΔSCB− Δprostokątny i SC jest wysokością a jej rzut na podstawę to CD ΔSAB−Δprostokątny i SA jest wysokością a jej rzut na podstawę to AD stąd tak zaznaczone kąty. Na rysunku Tomka też ładnie widać.

Mila: Może Bogdan tu spojrzy i lepiej ( inaczej) wytłumaczy.

Przyszly_Makler: Milu, a skoro SA jest wysokością to kąd DAS, nie powinien być też prosty? PS. Dziękuję wszystkim za starania staram się wszystko przeanalizować.

Mila: Na Twoim rysunku tak.

Przyszly_Makler: W Twoim poście z 21:39 napisałaś "ΔSAB−Δprostokątny i SA jest wysokością a jej rzut na podstawę to AD" to chyba Ci chodziło, że SD jest wysokością, tak? [wedle oznaczeń Twoich]

Mila: SD− wysokość ostrosłupa SA jest wysokością w ΔSAB, jej rzut ( oświetlasz z góry) na pł.podstawy to AD.

Przyszly_Makler: wydaje mi się, że zrozumiałem... w sumie to się cieszę, ale nie jestem pewien, czy to rozumiem. Dziękuję wszystkim za pomoc, a Milu mogłabyś mi jeszcze powiedzieć skąd wiadomo w tym zadaniu https://matematykaszkolna.pl/strona/3669.html że wysokość ostrosłupa leży na wysokości podstawy?

Mila: ściana boczna i podstawa to Δrównoramienne w dodatku przystające.

PrzyszlyMakler: I ze tak zapytam jako niedouczony uczeń, na mocy jakiego prawda sprawia to, że wysokość właśnie leży na wysokości podstawy ?

Mila: Jeżeli "złożysz " ostrosłup wzdłuż BC to trójkąty BCS i BCA pokryją się. W zależności od długości AS rzut S na tę wysokość podstawy będzie w różnych punktach.

PrzyszlyMakler: Czyli.. jeżeli dwie z 4 ścian ostrosłupa to trójkąty rownoramiennne to spodek jego wysokości zawsze leży na wysokości podstawy ?

Mila: Nie wiem, zależy od ostrosłupa , związków miarowych. Na ogół w zadaniach masz dość jasne sformułowanie z którego wnioskujesz, gdzie leży spodek wysokości ostrosłupa.