wyznacz wartości parametru m Monika: Wyznacz wszystkie wartości parametru m, dla których prosta o równaniu y=x−3 dzieli trójkąt abc o wierzchołkach A(1,1) B(2,3) C(m,1) na dwie figury o równych polach.

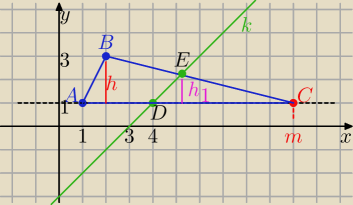
Eta: 1/ Umieść punkty w układzie współrzędnych i narysuj prostą y=x−3 2/ Punkt D ∊k y= x−3 i należy do prostej AC : y=1 zatem D( 4,1) to m >4

	1
3 / P(ABC) =		*h*|AC| , h= 2 , |AC|= m−1 i m>4
	2

P(ABC)= m−1 4/ z treści zadania P(ABC)=2P(DCE) 5/ Napisz równanie prostej BC : przechodzącej przez punkty B(2,3) i C(m,1) 6) rozwiąż układ równań prostych k i BC otrzymasz współrzędne punktu E .........

	6m−8		3m−8
xE=		, yE=
	m		m

	6m−8		2m−8		2(m−4)
h1 trójkąta DEC : y=xE −3−1=		−4 =		=
	m		m		m

	1
P(DEC)=		*|DC|*h1 , |DC|= m−4 i m>4 ,
	2

	m−4)2
P(DEC)=
	m

ponieważ P(ABC)= 2P(DEC) to:

	2(m−4)2
m−1=		i m>4 ⇒ m = .......................
	m

rozwiąż to równanie i uwzględnij ,że m>4 i to wszystko