Oblicz sinx, cos, tg, jeśli... uczeń123:

	−3π		1
1. Oblicz sinx, jeśli x ∊ (		, 0) i cosx =
	2		3

	π		2
2. Oblicz cosx, jeśli x ∊ (		, 2π) i sinx =
	2		3

	1
3. Oblicz tgx, jeśli x ∊ (0, π) i cosx =
	4

Jerzy: Skorzystaj z jedynki trygonometrycznej. Przedział pozwoli ustalić znak wyniku.

uczeń123:

	2√2
W 1. wyszło mi, że sinx =		. Jest ok?
	3

Jerzy: Wartość dobra, ale w tym przedziale sinus jest zrówno dodatni, jak i ujemny,więc daj dwie odpowiedzi.

uczeń123:

	2√2		2√2
1.		i −
	3		3

	√5
2.		?
	3

Jerzy: 1) ... lub .... 2) Też +/−

uczeń123: Może to głupie, ale...jak porównywać otrzymany wynik do przedziału w którym jest x?

Jerzy: Sprawdzamy, czy w podanym przedziale funkcja jest dodatnia, czy ujemna .

uczeń123: To rozumiem (wierszyk o ćwiartkach), ale chodzi mi bardziej o to jak interpretować np.

	2√2		3π
		w przedziale (		, 0)? Wynik jest liczbą, a "x" przedziałem "kątowym".
	3		2

Jerzy:

	2√2
Nie ... x to ten argument, dla którego cosx =
	3

uczeń123: Pokażesz mi jak to widzisz?

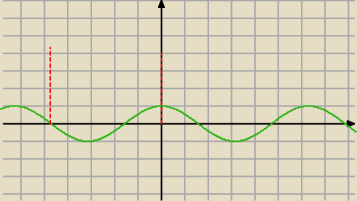
Jerzy: Widać,że w przedziale (−270,0) cosinus przyjmuje wartości dodatnie i ujemne.

uczeń123: (−270,0)?

Jerzy: Tak, taki masz przedział w zad 1)

uczeń123: No tak, po zamianie miary łukowej. Czyli dla 2. patrzymy na przedział (90,360) i widzimy że cos osiąga wartości i dodatnie i ujemne?