Pomoc Sky: Mógłby ktoś sprawdzać obliczenia i czy dobrze robię? Dane są punkty A=(−2,−4), wyznacz rownanie prostej w ktorej zawarta jest symetralna odcinka AB. Wyznacz pole koła, którego odcinek AB jest średnicą.

⎧	−4=−2a+b
⎩	6= 4a+b

⎧	4=2a+b
⎩	6−4a+b

10=6a

	5
a=
	3

	5
6= 4*		+b
	3

	20
6−		+b
	3

13		20
	−		+b
3		3

	2
−		= b
	3

	5		2
y=		x−
	3		3

Sky: Poprawka w treści! Dane są punkty A=(−2,−4), B=(4,6)

Janek191: Brak punktu B

Sky: Już dopisany wyżej

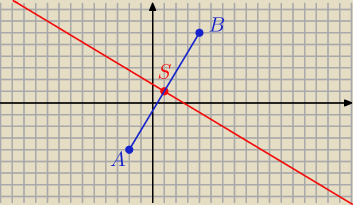
Janek191: S = ( 1, 1)

	6 − (−4)		10		5
a =		=		=
	4 − (−2)		6		3

	5
y =		x + b
	3

	3
a1 = −
	5

	3
y = −		x + b
	5

	3
1 = −		*1 + b
	5

5		3
	+		= b
5		5

	8
b =
	5

	3		8
y = −		+
	5		5

===================

Sky: Teraz widzę ile błędów popełniłam przy przepisywaniu rozwiązania, ale mam nadzieję, że ktoś się domyśli

Sky: Aha... czyli jednak dobrze, że kazałam sprawdzić

Janek191: r = 0,5 I AB I → AB = [ 6, 10] I AB I = √6² + 8² = 10 r = 5 P = π r² = 25 π =============

Sky: Dziękuję wybawco!

Janek191: Umiesz obliczyć S ?

Sky: Ale dlaczego S jest (1,1)?

Sky: no właśnie nie

Janek191: A = ( x₁, y₁} B = ( x₂, y₂} wtedy prosta AB

	y2 − y1
a =
	x2 − x1

y = a x + b

	x1 + x2		y1 + y2
xs =		ys =
	2		2

S = ( x_s, y_s} − środek odcinka AB

Sky: Jeszcze raz dziękuję

Janek191:

	− 2 + 4		2		− 4 + 6
xs =		=		= 1 y1 =		= 1
	2		2		2

Janek191: Miało być y_s

Janek191: y = a x + b Prosta prostopadła do niej

	−1
y = a1 x + b1 gdy a*a1 = − 1 ⇒ a1 =
	a

Sky: Ok, już wszystko rozumie