ekstrema zef: Mam funkcję:

	10x
f(x)=		dla x∊(0;10)
	x2+1

I mam wyznaczyć największa i najmniejszą wartość w tym przedziale liczę pochodną:

	−10x2+10
f'(x)=
	(x2+1)2

przyrównuję do zera

−10x2+10
	=0
(x2+1)2

x=1 lub x=−1 Zostaje mi x=1 bo x=−1 odpada ze względu na założenie co do przedziału funkcji f(1)=5 Sprawdzam też końce przedziałów, a skoro są otwarte to liczę granice:

	10x		0+
lim		=		=∞
	x2+1		1

x→0⁺

	10x		100
lim		=
	x2+1		101

x→10⁻ No i według mnie to maks=5 a co z minimum ? może ktoś pomóc ?

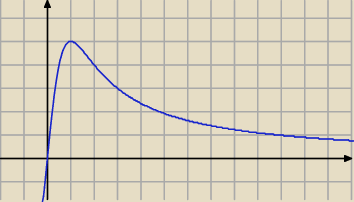
Janek191: Ze względu na otwarty przedział ( 0, 10) funkcja nie ma najmniejszej wartości ani minimum lokalnego. Granica źle obliczona. 0 : 1 = 0

zef: Aha rozumiem Jeżeli pochodna zeruje się w pewnym x_o który nie należy do przedziału f(x) to nie będzie tam ekstremum, ale za to może być jakaś najmniejsza wartość w tym przedziale tak ?

Janek191: Tak, ale w przedziale domkniętym

zef: Dziękuję bardzo

zef: Mam problem z innym przykładem: Wyznacz wartości (o ile istnieją) funkcji f: największa (M) i najmniejszą (m) w podanym zbiorze:

	1
f(x)=		, x∊<1;2)u(2;3>
	x2−4

Liczę pochodną:

	−2x
f'(x)=
	(x2−4)2

Przyrównuję do zera co daje mi x=0 który nie należy do przedziału. Czyli sprawdzam punkty skrajne przedziałów= 1 i 3

	1
f(1)=−
	3

	1
f(3)=
	5

	1		−1
Czyli M=		, m=
	5		3

W odpowiedziach jest jednak że M i m nie istnieją, dlaczego ?

zef:

zef: Pomoże ktoś ?

zef:

Mila:

	1
limx→2−		=−∞
	x2−4

	1
limx→2+		=∞
	x2−4

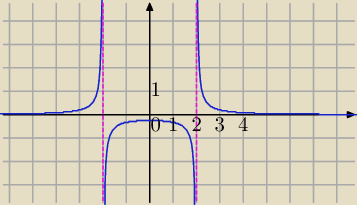
Zatem w podanym zbiorze nie istnieje najmniejsza wartość i tak samo największa nie istnieje. Ty obliczyłeś osobno w każdym z przedziałów. I tak w przedziałe <1,2) istnieje największa, nie istnieje najmniejsza.

zef: Hmm, trochę dalej nie rozumiem. Licząc te granice zostało udowodnione, że w 2 funkcja ta nie jest ciągła, ale dalej nie kumam czemu nie mogę liczyć tego poprostu f(1) i f(3)

zef: Aha, chyba już wiem. Rozpatrując 2 przedziały otrzymujemy +∞ i −∞ co oznacza że nie ma ani wartości maksymalnej ani minimalnej, ja chyba sprawdzałem dla dwóch tak jakby oddzielnych przedziałów

Mila: To właśnie napisałam, ale chyba, nie doczytałeś.

zef: Tak, już widzę, jeszcze raz dziękuję bardzo !