Orientacja Benny: Jak mam powierzchnie stożka x²+y²=z², 0≤z≤R to jaka jest orientacja wektora normalnego tej powierzchni?

Adamm: zakładam że chodzi o sam stożek, bez podstawy jeśli dla wektora normalnego z<0 to pozytywna, a jeśli z>0 to negatywna

Saizou : Za wektor normalny możesz przyjąć gradient F(x,y,z)=x²+y²−z²=0 grad(F)=(2x, 2y, −2z)

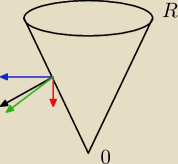
Adamm: wystarczy spojrzeć na stożek jeśli orientacja jest dodatnia to od razu widać że składowa z wektora normalnego musi być ujemna

Benny: No to czegoś nie rozumiem. Skoro mam w treści zadania, że powierzchnia stożka jest zorientowana dodatnio to powierzchnia jest zorientowana zgodnie z wektorem.

Benny: ∫∫x²dydz+y²dzdx+z²dxdy, po powierzchni stożka to korzystając z G−O

	1
2∫∫∫(x+y+z)dzdxdy=2∫∫(x√x2+y2+y√x2+y2+x2+y2)dxdy=		πR4, a mam pokazać, że tak
	2

	−πR4
całka jest równa
	2

Saizou : A może cała treść zadania ?

Benny: Korzystając ze wzoru Gaussa−Ostrogradzkiego wskazać, że gdy δ jest zewnętrzną częścią powierzchni {(x,y,z,):x²+y²=z², 0≤z≤R}, to

	−1
∫∫δx2dydz+y2dzdx+z2dxdy=		πR4
	2

Saizou : no to teraz współrzędne biegunowe i oblicz tę całkę

Benny: No to wychodzi mi wynik taki sam, ale z innym znakiem.

Benny: Hmm?

Benny: :(

jc: Zmień kolejność parametrów, jakobian zmieni znak i będziesz miał minus

Benny: Czemu zamienić kolejność parametrów?

jc: Ja bym się nie przejmował, tylko postawił znak minus. Zwykła całka objętościowa jest dodatnia (całkujesz funkcję dodatnią).

Benny: Wydaje mi się że w treści jest błąd. Z taką treścią na pewno dostaniemy wartość dodatnią, bo powierzchnia jest zorientowana dodatnio. Co o tym myślisz?

jc: Benny, bardziej zainteresowałeś mnie liczbami Gaussa.

Benny: W jaki sposób?

jc: A to nie Ty pytałeś o algorytm Euklidesa i liczby postaci a+bi, gdzie a i b są całkowite?

Benny: Oczywiście, że ja choć nadal nikt się nie wypowiedział w temacie, ale mam inne rzeczy jeszcze do roboty, więc to ewentualnie może poczekać