Ekstrema zef: Chodzi o przykład 2.97 a https://pl-static.z-dn.net/files/de6/e7de726443a3a6a772553c31cc29cf69.jpg Policzyłem wszystkie ekstrema i dodatkowo sprawdziłem ciągłość funkcji w punkcie x=−2 ( jest ciągła ) Jak sprawdzić czy w tym punkcie x=−2 jest ekstremum lokalne ?

Adamm: porównaj pochodną z lewej oraz z prawej

zef: Mógłbyś mi to dokończyć ? pochodne to: 3x²+16x+21

10x
(x2+1)2

Adamm: f'₋(−2)=1

	4
f'+(−2)=−
	5

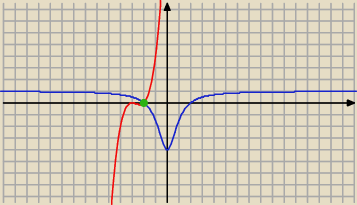
więc mamy maksimum w punkcie x=−2, co ilustruje rysunek

zef: Ok rozumiem, policzyłeś pochodne obustronne w punkcie x=−2 ale skąd wiesz że to jest maksimum ? Da się to bez wykresu zrobić ?

Adamm: bo są różnych znaków pochodne są oczywiście ciągłe, więc tym się nie przejmujemy pomyśl, funkcja rośnie (co mówi nam pochodna lewostronna) i potem nagle maleje, musi tam być maksimum

qwe: a po co sprawdzasz ciągłość funkcji?

zef: Dziękuję, rozumiem !

Adamm: qwe, aby funkcja była różniczkowalna potrzeb aby była ciągła