zadanie optymalizacyjne :*: Proszę o pomoc. Długość przeciwprostokątnej w trójkącie prostokątnym jest równa 20 cm. jakie powinny być długości przyprostokątnych tego trójkąta aby kwadrat długości wysokości poprowadzonej z wierzchołka kata prostego miał największą wartość?

Janek191:

:*: i co dalej z tym zrobić?

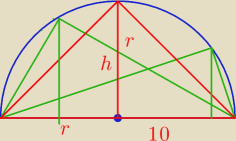
Janek191: c =2 r = 20 Z rysunku widać, że h = r = 10 Wtedy a = b = 10√2

:*: takie średnie to rozwiązanie bo jak można powiedzieć że cos wynika z rysunku. na maturze nie przejdzie

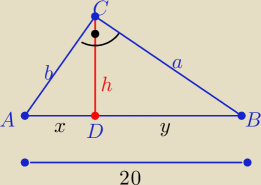
Eta: x+y=20 ⇒ y=20−x , x∊(0,20) h²=x*y⇒ h²(x)=x(20−x) = −x²+20x −−− parabola ramionami do doału to h²(x) osiąga największą wartość dla odciętej wierzchołka paraboli

	−20
xmax=		= 10 wtedy y= 20−10=10
	−2

to h²=100 ⇒ h=10 czyli trójkąt ABC jest prostokątny równoramienny o ramionach a=b= 2√10 cm

:*: dlaczego w drugiej linijce jest że h²=X*Y. A poza tym wszystko rozumiem dzięki piekne

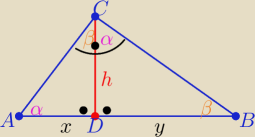
Eta: Z podobieństwa trójkątów ADC i DBC z cechy (kkk)

h		y
	=		⇒ h2=x*y
x		h

Warto pamiętać tę zależność ( jest też ujęta w karcie wzorów ... patrz trójkąt prostokątny

:*: dziękuję bardzo

Eta: Na zdrowie ....