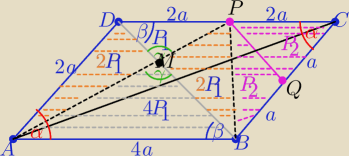
Równoległobok Werr: Witam. Pilnie potrzebuje pomocy z tym zadaniem. Dany jest równoległobok ABCD w którym |AB|=2|AD|, a przekątne maja długość 2√2 i 4√2 Oznaczmy środki bokow BC i DC odpowiednio jako punkty Q i P. A) oblicz pole równoległoboku ABCD b) oblicz pole czworokata ABPQ

Eta: |AC|=f=4√2 i |BD|=e=2√2 , a>0 W każdym równoległoboku : f²+e²=2|AB|²+2|AC|² ( możesz wykazać z tw. kosinusów to 40a²=40 ⇒ a=1 to |AB|=|DC|=4 i |AD|=|BC|=2

	1
|PQ|=		|BD|= √2
	2

	42+22−(2√2)2		3
z tw. kosinusów w ΔABD : cosα=		=
	2*4*2		4

	9		√7
to sinα= √1−		=
	16		4

a) P(ABCD)= |AB|*|AD|*sinα=.... = 2√7 [j²] b) w trapezie ABPD ΔABM∼ ΔDPM z cechy (kkk) w skali k=2 P(DPM)=P₁ , P(ABM)= 4p₁ , P(ADM)=P(BPM)= 2P₁

	√7
to P(ABCD)= 8P1 ⇒ P1=
	4

	1		√7
P(CPQ) =P2 ⇒ P2=		P(ABD) ⇒ P2=
	4		4

	5√7
P(ABPQ)= 6P1+P2 =.............. =		[ j2]
	4

Werr: Dziękuję!

Eta: Widzę,że podczas przepisywania wkradł się chochlik

	√7
poprawiam P(ABCD)=12P1 ⇒ P1=
	6

reszta .... ok

5-latek: I jeszcze jeden chochlik jest Powinno byc +2|AD|² a nie +2|AC|² .