:PP Dziąku: Prosiłbym o pomoc Bardzo nie lubię zadań związanych z geometrią itp, od zawsze więc prosiłbym o pomoc. Dział : Przystawanie trójkątów Zad 1: W trójkątach ABC i A'B'C' poprowadzono środkoweBD i B'D'. Wykaż że jeśli |BC|=|B'D'| , |BC|=|B'C'| oraz |kąt DBC|=|kąt D'B'C'| to trójkąt ABC = trójkąt A'B'C' zad2: W trójkątach ABC i A'B'C' poprowadzono dwusieczne CD i C'D'. Uzasadnij że trójkąt ABC = trójkąt A'B'C' wiedząc że |CD| = |C'D'|, |DA|= |D'A'| oraz |kąt CDA| = |kąt C'D'A'| Zad 3: W trójkątach ostrokątnych ABC i A'B'C' poprowadzono wysokości CD i C'D'. Wykaż że trójkat ABC = trójkąt A'B'C' jeżeli |kąt A| = |kat A'| , |kąt B| = |Kąt B'| i |CD| = |C'D'| te kolorkiem czewonym te równa się to są 3 KRESECZKI nie dwie , Prosiłbym o pomoc. Pozdrawiam

Dziąku: POnawiam

Dziąku: ponawiam

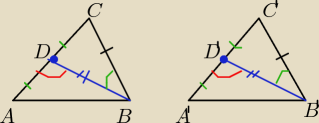
Aramis: 1) IDBI = ID^'B^'I i IBCI = IB^'C^'I i I< DBCI = I< D^'B^'C^'I to z cechy ( b,k,b) ΔBDC = ΔB^'D^'C^' zatem : I<BDCI= I<B^"D^'C^'I to w ΔABD i ΔA^'B^'D^' I<ADBI = I<A^'D^'B^.I = 180^o− I<BDCI i IDBI= ID^'B^'I i IDCI = IADI = IA^'D^'I to Δ ABD = ΔA^'B^'D^' z cechy (b,k,b) więc ΔABC= ΔA^'B^'C^' ( zamiast znaku = napisz znaki przystawania "trzy kreseczki") Pozostałe dwa zadania podobnie 2) z cechy najpierw z cechy (b,k,b) a później z cechy (k,b,k) 3) dwa razy z cechy (k,b,k) powodzenia