geometria analityczna, obliczanie wierzchołków kasiaszek: Witam, mam takie zadanie:

	1
Boki AB i AC trójkąta ABC zawierają się odpowiednio w prostych y=−		x i y=x+3. Oblicz
	2

współrzędne wierzchołków trójkąta, jeśli dany jest środek S(4,1) odcinka BC. Policzyłam współrzędne punktu A, ale nie wiem, co dalej, czy mógłby mnie ktoś naprowadzić? Widziałam już takie podobne zadanie, gdzie druga prosta to x=0, więc dwa punkty znajdują się na tej samej prostej. Co w takim razie w tej sytuacji, gdy dwie proste są nachylone pod jakimś kątem?

kasiaszek: pomoże ktoś?

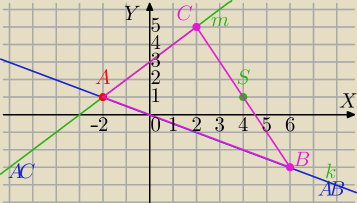
Mila: Wierzchołek A należy do obu prostych (?)

	1
k: y=−		x
	2

i m: y=x+3

	1
−		x=x+3
	2

A=(−2,1)

	1
B∊k⇔ B=(b,−		b)
	2

C∊m⇔C=(c,c+3) S=(4,1) jest środkiem BC zatem:

	b+c		−0.5b+c+3
4=		i 1=
	2		2

b+c=8 −0,5b+c+3=2 −−−−−−−−− b+c=8 −0,5b+c=−1 b=6 i c=2 A=(−2,1), B=(6,−3) i C=(2,5)

kasiaszek: dzięki wielkie, coś z tym kombinowałam, byłam blisko, ale ostatecznie nie wpadłam, kręciłam się w kółko xD jeszcze raz dzięki!

Mila: Czy to zgodne z odpowiedzią?