rozwiąż równanie dla x od zera do pi
pomocy: tg x + ctg x ≥ 4sin 2x
12 sty 17:39
pomocy: wyszło mi że x∊<−712π + kπ; π12+kπ>
uwzględniając x∊(0; π)
wyszło mi x∊<512π; π) a to jest błędny wynik
12 sty 17:42
pomocy: co zrobiłem źle?
12 sty 17:44
pomocy: zależy mi na czasie, proszę o szybkie wyjaśnienie

12 sty 17:45
pomocy: ktoś coś?
12 sty 17:57
pomocy: 23 minuty i znikąd pomocy

12 sty 18:02
Benny: Skąd mamy wiedzieć co zrobiłeś źle skoro podałeś tylko wynik. Pokaż jak liczysz coś poradzimy.
12 sty 18:11
lol: rozwiążcie mu to zadanie chociaż z obliczeniami, też mam takie i nie wiem
12 sty 19:01
Mila:
Liczę. Cierpliwości.
12 sty 19:12
Mila:
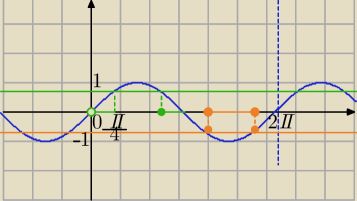
x∊(0,π)
| sinx | | cosx | |
| + |
| ≥4sin2x |
| cosx | | sinx | |
| sin2x+cos2x | |
| ≥4sin(2x) |
| sinx*cosx | |
| 2 | |
| ≥4sin(2x) /*sin2(2x) |
| sin(2x) | |
2sin(2x)−4sin
3(2x)≥0
2sin(2x)*(1−2sin
2(2x))≥0
sin(2x)=t i |t|≤1 i t≠0
t*(1−2t
2)≥0⇔t*(1−
√2t)*(1+
√2t)≥0⇔
| | √2 | | √2 | |
t∊<−1,− |
| > lub t∊(0, |
| >⇔ |
| | 2 | | 2 | |
| | π | | 3π | | 5π | | 7π | |
0<2x≤ |
| lub |
| ≤2x≤π lub |
| ≤2x≤ |
| /:2 |
| | 4 | | 4 | | 4 | | 4 | |
| | π | | 3π | | π | | 5π | | 7π | |
0<x≤ |
| lub |
| ≤x≤ |
| lub |
| ≤x≤ |
| |
| | 8 | | 8 | | 2 | | 8 | | 8 | |
=================================
12 sty 19:24


 x∊(0,π)
x∊(0,π)