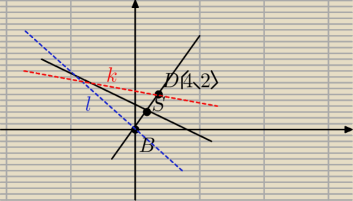
ROMB PrzyszlyMakler: Punkty B= (0,0) i D=(4,2) są wierzchołkami kątów rozwartych rombu ABCD. Kąt ostry rombu ma miarę 60. Napisz równanie okręgu wpisanego w ten romb. Bez trudu wyznaczam środek okręgu, czyli miejsce przecięcia przekątnych czyli środek symetii. S(2,1) Prosta BD ma równanie: 2=4a +b b=0

	1
a=
	2

Prosta prostopadła do prostej BD przechodząca przez punkt S: y=−2x +b ∊ S(2,1) 1= −4 + b b = 5 Prosta, w której leżą pozostałe wierzchołki, a zarazem przekątna tego rombu ma równanie y=−2x +5 Pozostałe wierzchołki rombu mają współrzędne postaci A(a, −2a + 5) Wystarczy mi jeden z nich, co pozowli mi napisać równanie prostej AB, a potem obliczę odległość prostej AB od S i będę miał pormień, jednak do tego musze wykorzystać informację, że kąt ostry ma 60 stopni, ale w ogóle nie potrafię tego zrobić.. Niby a = tg60 , czyli √3, ale trochę tego nie rozumiem, bo rysując rysunek pomocniczy wiem, że ta prosta nie będzie równoległa do OX, więc trochę to skomplikowane. I nie rozumiem której prostej to będzie współczynnik.. tej oznaczonej przeze mnie na rysunku jako k czy l? Bo to właśnie kąt pomiędzy kl ma 60 stopni. Niby też wiem, że kąt pomiędzy l, a prostą y=−2x +5 to 30 stopni (bo przekątna jest też dwusieczną), ale nie wiem jak to wykorzystać, mimo wszystko.

PrzyszlyMakler: Wpadłem na pomysł, że skoro przekątne są dwusiecznymi to, ten trójkąt musi być równoboczny ABD. Prawidłowe zalożenie i wszystko? I mając długość przekątnej BD, wiem, że BA i DA są takiej samej długości i z tego mogę policzyć współrzędne A. Potem równanie prostej BA i jej odległośc od punkt S będzie promieniem. Czy to dobry pomysł? A żeby się nie zmarnował temat, mógłby mi ktoś wyjaśnić co mi daje kąt jakiejś prostej w zadaniach, jeżei ta prosta nie jest równoległa do OX?

PrzyszlyMakler: refresh

Jerzy: Kombinujesz jak końpod górę. Masz środek okręgu, więc potrzebujesz jeszcze promień.

	r
Zauważ,że:		= tgα , gdzie α to kąt jaki tworzy prosta BD z osią OX.
	1   |DB| 2

I po zadaniu.

Jerzy: Sorry ... pomyłka.

PrzyszlyMakler:

	r
Skąd to wiesz?		to tgβB i mogę się zgodzić, że to też jest tg 60 stopni, ale z tym
	1/2DB

mam problem, skąd mam wiedzieć, że to tg prostej BD a nie AD? wiem, że dziwne pytanie, ale zależy mi na tym aby to zrozumieć.

PrzyszlyMakler: sorry, r/1/2 DB to sinβ

Jerzy: Inaczej ... przekątne rombu się połowią. Masz długość przekatnej BD i masz prostą zawierającą przekatną AC

	1
Ze środka okręgu S(2,1) poprowadź okrag o promieniu		|BD|,
	2

punkty przecięcia z prostą AC wyznaczą pozostałe dwa wierzchołki.

PrzyszlyMakler: Wow..... a z czego to wynika, jak na to wpasc?

Jerzy: Ale co wynika ?

Jerzy: Dalej źle... muszę pogłówkować

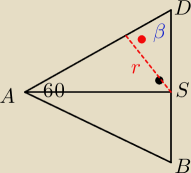
PrzyszlyMakler: To, że miejsca przecięcia okręgu wpisanego w romb z okręgiem opisanym na jego przekątnej wyznaczają wierzchołki rombu. A tak poza tym, to już zrobiłem to zadanie . Zrobiłem z mojego rysunku z 12:55. kąt SDA to 30 stopni, to kąt b to 60 stopni czyli sin60 = U[r}{DS} a dł. odcinka DS możemy łatwo policzyć i wynik mi wychodzi jak w odpowiedzi

PrzyszlyMakler:

	r
kąt β to 60 stopni, czyli sin 60=		i z tego prosto wychodzi wyniki.
	DS

Jerzy, a skąd wiesz kiedy Twoje sposoby są złe? Sprawdzasz jakoś programem czy co ?

Jerzy:

	1
Po prostu z rozpędu napisałem,że promień okręgu pomocniczego to :		|BD|,
	2

a tak wcale nie musi byc

PrzyszlyMakler: Ale jakoś sobie poradziliśmy. Dzięki za próby, w sumie bez Ciebie bym nie narysował tego rysunku i nie zobaczył jak prosto to można zrobić. Jak to jest narysowane pod kątem w układzie współrzędnych to ciężko dostrzec te banały

Jerzy: To Ty sobie poradziłeś

relaa: Połowa rombu, czyli rysunek Pana to trójkąt równoboczny, zatem |AB| = |AD| = |BD| = 2√5 p = 4√5

	π
PABCD = (2√5)2 • sin(		) = 10√3
	3

	P		10√3		√15
r =		=		=		.
	p		4√5		2