okrag i kwadrat PrzyszlyMakler: W prostej o równaniu 2x+y−6=0 zawiera się bok kwadratu opisanego na okręgu o równaniu x²+y²−2y−4=0 . Oblicz współrzędne wierzchołków tego kwadratu. układ równań: y=−2x + 6 (x−1)² + y² = 5 rozwiązanie tego układu pozowli mi obliczyć punkt styczności prostej z okręgiem, czyli punkt styczności prostej ze środkiem boku jednego kwadratu. Tylko... rozwiązując to równanie (x−1)²+(6−2x)²=5 5x² −26x + 32 = 0 Δ=36 x₁= 3,2 y₁ = −0,4 x₂=2 y₂= 2 I tutaj moje pytania: 1. Dlaczego wyszły dwie odpowiedzi? Przecież ta prosta ma być styczna do okręgu w jednym punkcie... 2. jak wyeliminować jedną z odpowiedzi?

5-latek: A kto powiedzial z eto ma byc styczna ? Zrobiles rysunek do zadania ?

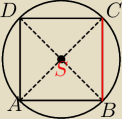
5-latek: Distaniesz taka sytuacje Jeden bok bedziesz mial dany

5-latek: I rownanie okregu bedzie takie x²+(y−1)²=5 czyli srodek okregu (0,1) i promien r=√5

PrzyszlyMakler: 5− latku. Kwadrat jest opisany na okręgu.

PrzyszlyMakler: Aha. Już widzę błąd. Nie ważny temat, delta wyjdzie 0.. napisałem (x−1)² a to (y−1)²/ Izi, sorki

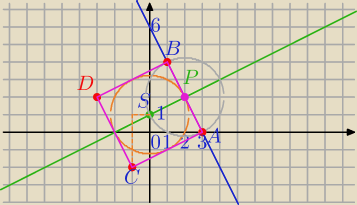
Mila: k: 2x+y−6=0⇔y=−2x+6 x²+y²−2y−4=0⇔ x²+(y−1)²=5, S=(0,1) r=√5

	|2*0+1*1−6|		5
d(S,k)=		=		=√5 zgadza się
	√22+12		√5

m⊥k i S∊m

	1
y=		x+1
	2

1
	x+1=−2x+6
2

x=2 i y=2 P=(2,2) punkt styczności okręgu z prostą k 2) współrzędne wierzchołków: y=−2x+6 i (x−2)²+(y−2)²=5 A=(3,0),B=(1,4) C i D wyznacz z symetrii względem S a=2√5− długość boku kwadratu