Czy da się wyznaczyć równanie prostej symetrycznej względem innej? not4you: Jak wyznaczyć równanie prostej symetrycznej do y=1/7x +25/7 względem prostej y=1/2x? Jest to możliwe? Jest to krótki fragment dosyć złożonego zadania z olimpiady AGH i zastanawiam się czy jakoś da radę? Mógłbym ewentualnie wyliczyć jeden punkt, przez który będzie przechodzić, jeśli to pomoże.

Janek191: Znajdź punkty wspólne danej prostej z dwiema prostymi prostopadłymi do prostej y = 0,5 x, a następnie znajdź ich obrazy w symetrii względem tej prostej. Te obrazy wyznaczą prostą symetryczną.

not4you: Dzięki za pomoc!

Janek191:

	1		25
k : y =		x +
	7		7

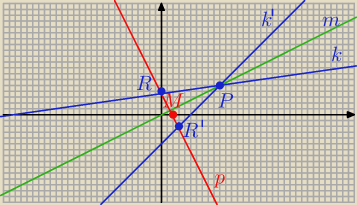
m : y = 0,5 x

	1		25
0,5 x =		x +		/ * 14
	7		7

7 x = 2 x + 50 5 x = 50 x = 10 y = 5 P = ( 10, 5) ============

	25
Dla x = 0 jest y =
	7

	25
R = ( 0,		)
	7

Prosta prostopadła do prostej m przechodząca przez R y = −2 x + b

25		25
	= − 2*0 + b ⇒ b =
7		7

	25
p: y = −2 x +
	7

−−−−−−−−−−−−− Punkt wspólny prostych m i p

	25
0,5 x = −2 x +		/ * 14
	7

7 x = − 28 x + 50 35 x = 50

	50		10
x =		=
	35		7

	5
y =
	7

	10		5
M = (		,		)
	7		7

	25
Szukam punktu symetrycznego do R= (0,		względem punktu M
	7

Mamy

0 + x		10		20
	=		⇒ x =
2		7		7

25   + y   7		5		25		10		15
	=		⇒		+ y =		⇒ y = −
2		7		7		7		7

	20		15
R ' = (		, −		)
	7		7

Prowadzę prostą przez punkty: R ' i P = ( 10, 5) y = a x + b

	15		20
−		=		x + b / * 7
	7		7

1) − 15 = 20 a + 7 b 5 = 10 a + b / * 2 2) 10 = 20 a + 2 b −−−−−−−−−−−−−−−−− Od 2) odejmuję 1) 25 = − 5 b ⇒ b = − 5 5 = 10 a − 5 ⇒ 10 a = 10 ⇒ a = 1 Odp. y = x − 5 ============