własności f. kwadratow. Natiss.x3: O funkcji kwadratowej wiadomo, że dla argumentu x = −1 przyjmuje wartość największą równą 4 oraz jednym z miejsc zerowych jest −3. a)podaj zbiór wartości − czy zbiór wartości to (−∞, 4> ? b) wyznacz drugie miejsce zerowe − nie umiem c) podaj zbiór wszystkich argumentów, dla których przyjmuje ujemne wartości− nie umiem d) podaj maksymalny przedział, w którym jest rosnąca − nie umiem e) wyznacz wzór w postaci iloczynowej/kanonicznej − nie umiem Proszę chociaż o wskazanie co i jak.

pikolo: A nie ma podanego żadnego wzoru tej funkcji?

Natiss.x3: Nie właśnie, mam go wyznaczyć dopiero w e) Podobno a, b, c, d da się zrobić z rysunku, bez obliczeń

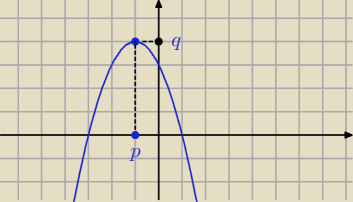
Janek191: a) p = − 1 q = 4 a < 0 x = − 3 y = a*( x − p)² + 4 = a*(x + 1)² + 4 a*(− 3 +1)² + 4 = 0 4 a = − 4 a = − 1 więc y = − ( x + 1)² + 4 =============== ZW = ( − ∞, 4 >

Janek191: ZW = ( − ∞, q > jeżeli q = f(p) jest wartością największą

parabola: x_w=p= −1 , y_w=q=4 i x₁=−3 to W(−1,4) A(−3,0)∊ do wykresu y=a(x+1)²+4 ⇒ 0=a(−3+1)²+4 ⇒ a= −1 y= −(x+1)²+4 −−− postać kanoniczna a) ZW= (−∞, 4>

	x1+x2
b)		=p ⇒ ...... x2= 1
	2

c) y↗ ⇔ x∊( −∞, p> ⇒ x∊.... d) y=a(x−x₁)(x−x₂) −−− postać iloczynowa y= .........

Janek191: b) x₁ = − 3 p = − 1 więc

x1 + x2
	= p
2

− 3 + x₂ = 2*(−1) = − 2 x₂ = − 2 + 3 = 1 ================= Lub x₂ − p = p − x₁ x₂ − (−1) = − 1 − (−3) x₂ + 1 = − 1+ 3 = 2 x₂ = 2 − 1 = 1 =============

Natiss.x3: b) p = x1 + x2/ 2 −1 = −3 + x2 / 2 −2 = −3 + x2 −2 + 3 = x2 x2 = 1 Dobrze?

Natiss.x3: O to mi się b udało

Natiss.x3: c) −(x + 1)² + 4 < 0 −(x² + 2x + 1²) + 4 <0 −x² − 2x + 3 < 0 Δ = 16 √Δ = 4 x1 = 1 x2 = −3 a to dobrze policzone?

Natiss.x3: tzn. funkcja przymue wartości uemne dla x = 1 i x = −3

Natiss.x3: a w d) p = −1 a<0 zatem (−∞, −1)

Janek191: c) f(x) < 0 ⇔ − (x + 1)² + 4 < 0 ⇔ (x + 1)² − 4 > 0 ⇔ (x+1)² > 4 ⇔ ( x+1 < − 2 lub x + 1 > 2 ) ⇔ ( x < − 3 lub x > 1 ) Patrz na wykres 19.44

Janek191: d) ( − ∞, p > = ( −∞, − 1 >