funkcje
Krzyś: Znajdź funkcję liniową f, która dla każdej liczby rzeczywistej r spełnia następujące dwa
warunki: f(2r)=2f(r)−1 i f(r+2)=4+f(r)
wiem że to zadanie już było i dostało odp. Ale dalej nie rozumiem, mógłby ktoś wytłumaczyć krok
po kroku?
10 sty 13:19
Adamm: f(2r)=2f(r)−1 ⇒ f(0)=2f(0)−1⇒f(0)=1
f(r+2)=4+f(r) ⇒ f(2)=4+f(0)
f(0)=1 ∧ f(2)=4+f(0) ⇒ f(2)=5
ponieważ mamy dwa punkty to mamy już prostą
10 sty 13:24
Adamm:
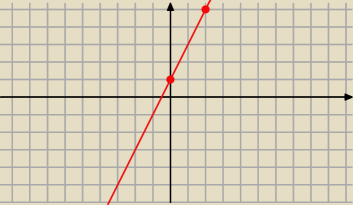
10 sty 13:26
Krzyś: ok zaczyna już mi coś świtać w głowie. W odp mam f(x)=2x+1 skąd się to wzieło?
10 sty 13:37
Jerzy:
Napisz równanie prostej przechodzącej przez punkty: (0,1) oraz (2,4)
10 sty 13:39
Jerzy:
Drugi punkt: (2,5) oczywiście.
10 sty 13:39
Krzyś: ok już mam dziękuję za pomoc

10 sty 13:44
Mila:
albo tak:
f(2r)=2f(r)−1 i f(r+2)=4+f(r)
f(x)=ax+b
1) f(2r)=a*2r+b i f(2r)=2*(a*r+b)−1⇔2ar+b=2ar+2b−1⇔b=1
f(x)=ax+1
2) f(r+2)=a*(r+2)+1=ar+2a+1 i f(r+2)= 4+a*r+1⇔ar+2a+1=ar+5⇔2a=4⇔a=2
f(x)=2x+1
10 sty 15:07
Jerzy:
Twój sposób
Mila jest bardziej "profesjonalny"

Witam

10 sty 15:10
Mila:
Witaj, wyjdzie to samo

10 sty 15:34
Jerzy:
Oczywiście, jakby mogło być inaczej. Co inna metoda, to inny wynik ?

10 sty 15:35


 Witam
Witam 

