monotonicznosc Metis: Znajdź przedziały monotoniczności f(x)= sinx+sin²x , gdzie x∊<0,2π> . f(x)= sinx+sin²x f'(x)=2sinx*cosx+cosx ⇔ cosx(2sinx+1) f'(x)=0 ⇔ cosx(2sinx+1)=0 cosx=0 v 2sinx+1=0

	1
cosx=0 v sinx=−
	2

	π		π
x=		v x=
	2		6

f'(x)>0 ⇔ cosx(2sinx+1)>0 f'(x)<0 ⇔ cosx(2sinx+1)<0 do tego momentu jest ?

Jack: po co Ci ekstrema do przedzialow monotonicznosci?

Metis: W zadaniu są też ekstrema Gorzej z rozwiązaniem tych nierówności

Jack: cosx = 0

	π		3
x =		lub x =		π
	2		2

	1
sin x = −
	2

	7		11
x =		π lub x =		π
	6		6

dla x ∊ <0;2π>

Jack: co do nierownosci to rozpatrz mniejsze przedzialy np.

	π		3π
1) dla cosx ≥ 0 czyli dla x ∊ <0;		> U <		;2π>
	2		2

2) dla cosx < 0 czyli dla pozostalych x

Metis: A sory, tam x∊<0,π> dlatego podałem tylko te rozwiazania

Jack: no to tym latwiej

Jack: ale to sinx = −1/2 nie ma rozwiazania w tym przedziale

Metis: Nie będzie maxa z tego kolokwium

Jack: a co, odbylo sie juz ?

Metis: Odbędzie się 10, ale nie uwzględniłem tego, że nie pamiętam trygonometrii, a tablic nie będzie

Jack: dasz rade !

Benny: Wszystko da się wyprowadzić

Metis: Benny w 45min to sobie mogę wyprowadzić ... wzór skróconego mnożenia

Jack: no chyba pamietasz jak wyglada funkcja sinx, albo cosx ?

Metis: No dobra, niby pamiętam, ale to nietrudny przykład, na kolosie będzie kilka a powinnienem to robić z automatu jak 2+2 , wiesz o co chodzi

Benny: No ja ostatnio nie miałem dostępu do internetu i zmuszony byłem wyprowadzić wzór na sumę cosinusów

Jack: Benny, wbij bys na chwile na gg?

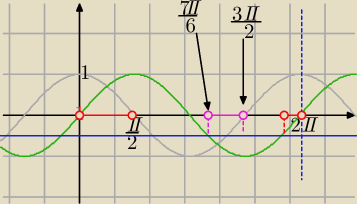
Mila: cosx*(2sinx+1)>0 i x∊<0,2π>⇔

	1
cosx>0 i sinx>−		( narysuj wykresy i odczytuj)
	2

	π		3π		7π		11π
x∊(0,		)∪(		,2π) i x∊(0,		)∪(		,2π)⇔
	2		2		6		6

	π		11π
x∊(0,		)∪(		,2π) (czerwone przedziały na osi)
	2		6

lub

	1
cosx<0 i (2sinx+1)<0⇔sinx<−
	2

	π		3π		7π		11π
x∊(		,		) i x∊(		,		)⇔
	2		2		6		6

	7π		3π
x∊(		,		) ( różowy przedział na osi)
	6		2

Metis: Dziękuje Milu, nie mam w tym biegłości

Metis: I mogę dać sobie rekę uciąć, że na kolokwium trafię na wzór trygonometryczny, tak to zawsze działa

Jack: ja na moim kolokwium to mialem jakis lnx *cos tam, juz nie pamietam, i mialem wyznaczyc funkcje odwrotna oraz monotonicznosc i ekstrema ;