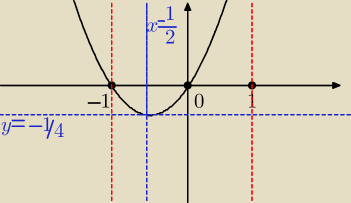
monotonicznosc Metis: Znajdź przedziały monotoniczności i ekstrema lokalne f(x). f(x)=cosx²+cosx Stosuję podstawienie t=cosx, gdzie t∊<−1,1> , mam zatem: f(t)=t²+t , gdzie t∊<−1,1> Funkcja kwadratowa, którą przekształcam do postaci kanonicznej:

	1		1
f(t)=(t +		)2−
	2		4

	1
f(t) maleje w przedziale <−1, −		>
	2

	1
rośnie w przedziale <−		, 1>
	2

	1
W t=−		mamy minimum
	2

Maksima osiągamy w pkt t=−1 i t=1 Przęchodzę do podstawienia: F(x) majeje, gdy

	1
−1≤ cosx≤−
	2

F(x) rośnie, gdy

	1
−		≤cosx≤1
	2

Maksima : cosx=1 i cosx=−1 Minimum

	1
cos=−
	2

Do tego momentu jest ?

Adamm: nie bardzo minimum, maksimum jest ok, monotoniczność już nie, z tego nie da się wywnioskować

Metis: Właśnie coś mi się nie zgadza

Metis: Czyli muszę działać bez podstawienia?

Adamm: tak

Metis: Nie ma efektywniejszego sposobu na taki przykład? f(x)=cos²x+cosx , x ∊<0,π> f'(x)=−2cosxsinx−sinx = −sinx(2cosx+1) f'(x)=0 ⇔ −sinx(2cosx+1)=0

	1
sinx=0 v cosx=−
	2

f'(x)>0 ⇔ −sinx(2cosx+1)>0 ⇔sinx(2cosx+1)<0 f'(x)<0 ⇔ sinx(2cosx+1)>0 straszneeee rachunki.

Adamm: kto wie? ten jest na pewno prosty

	1		−1
sinx(2cosx+1)<0 ⇔ (sinx<0 ∧ cosx<−		) ∨ (sinx>0 ∧ cosx>		)
	2		2

zauważ że wystarczy narysować wykres w przedziale 0 do 2π

Metis: Wątpie, że na kolokwium będę miał czas na wykresy Myślałem, że podstawieniem załatwię taki przykład w kilka minut

jc: Ja bym jednak bronił podstawienia. kosinus na pewnych przedziałach rośnie, na innych maleje. Ten przykład faktycznie jest prosty, ale można sobie wyobrazić coś dużo bardziej złożonego, gdzie dobre rozpoznanie złożenia rozwiązuje problem.

Metis: jc czyli jak zastosować w tym przypadku podstawienie, widzisz, że u mnie cos sie nie zgadza

Adamm: ja bym się nie skupiał na podstawieniach, a na samych ekstremach policz drugą pochodną i sprawdź

Adamm: potem masz od razu monotoniczność

Metis: Możesz mi pokazać jak to zrobić z użyciem II pochodnej?

Mariusz: Zadanie na pochodną ?

Mariusz: Druga pochodna to raczej wypukłość i punkty przegięcia chociaż jest taki wariant warunku wystarczającego f''(x)<0 maximum przy f'(x)=0 f''(x)>0 minimum przy f'(x)=0 ale to jest warunek wystarczający (dostateczny) poza tym gdy druga pochodna wyjdzie zero trzeba sprawdzać kolejne pochodne

Metis: Więc jak najszybciej "załatwić" to zadanie

Mariusz: Pierwsza pochodna załatwia wszystko Monotoniczność f'(x)>0 f(x) funkcja rosnąca f'(x)=0 f(x) funkcja stała f'(x)<0 f(x) funkcja malejąca f'(x)=0 warunek konieczny istnienia extremum Jeżeli w otoczeniu punktu gdzie f'(x)=0 pochodna zmienia znak z + na − to funkcja rosła a później maleje więc w punkcie mamy maximum Jeżeli w otoczeniu punktu gdzie f'(x)=0 pochodna zmienia znak z − na + to funkcja malała a później rośnie więc w punkcie mamy minimum