Oblicz pole obszaru ograniczonego wykresami funkcji Poloniusz: y=x²−1, y=x²+9

zef: Sprawdź czy dobrze przepisałeś funkcje.

Poloniusz: y=x²−1, y=−x²+9

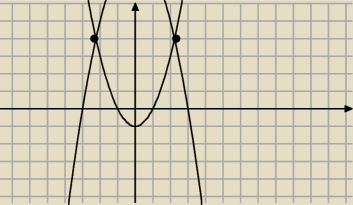
zef: Teraz lepiej. y₁=y₂ x²−1=−x²+9 2x²=10 x²=5 x=√5 lub −√5 − to będą granice całkowania. ∫_−√5^√5(−x²+9)−(x²−1)dx policz dalej

Adamm: x²−1=−x²+9 x²=5 x=±√5

	2
|∫−√5√5x2−1−(−x2+9) dx| = 2|∫0√52x2−10 dx |= 2 | [		x3−10x ]0√5
	3

| =

	10		40
= 2 |		√5−10√5 | =		√5
	3		3

zef: Adamm Rozumiem że zmieniłeś granice od 0 do √5 dlatego że jest zachowana symetria względem osi Y i pole po prawej i lewej stronie będą sobie równe tak ?