zadanie Metis: Gdzie popełniam błąd?

	3x+sinx
Znajdz wszystkie asymptoty f(x)=
	x

	3x+sinx
f(x)=		, gdzie x≠0
	x

Poszukuję dowodu istnienia asp. pionowej, stąd:

	3x+sinx		3x		sinx
lim		= lim		+		= 3
	x		x		x

x−>0−

	3x+sinx		3x		sinx
lim		= lim		+		= 3
	x		x		x

x−>0⁺ Granica w x−>0 jest własciwa więc asymptota pionowa(nawet jednostronna) nie istnieje. Poszukuję zatem asy. ukośnych( w tym poziomych), stąd:

	3x+sinx		1
lim		*		=
	x		x

x−>−oo

	−3x+sin(−x)		1
lim		*		=
	−x		−x

x−>oo

	−3x−sin(x)		1
lim		*		=
	−x		−x

x−>oo

	3x+sin(x)		1
lim		*		=
	x		−x

x−>oo

	3x+sin(x)		3x		sinx		1
−lim		= lim		+		*		=0
	x2		x2		x		x

x−>oo

	3x+sinx		1
lim		*		=0
	x		x

x−>oo a=0

	3x+sinx		3x+sinx
lim		−0*x=lim
	x		x

x−>oo

	3x+sinx		3x		sinx
lim		= lim		+		= 3
	x		x		x

x−>oo

	3x+sinx
lim		= 3
	x

x−>−oo Zatem y=3 jest jedyną asymptotą poziomą f(x). Ale po narysowaniu wykresu już tą asymptotą nie jest

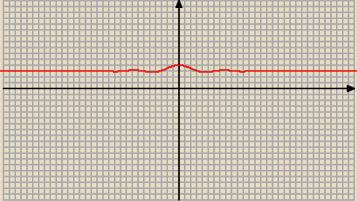
Adamm: nie jest?

Metis: http://prntscr.com/dt0ey2

Adamm: no i wygląda na to że dąży asymptotycznie do trójki z twojego screena

Metis: Ok , gdy się trochę cofnę , to jest

Metis: Zapis tego zadania prawidlowy?

Adamm: jest ok tylko przy liczeniu asymptot pionowych masz 4 zamiast 3

Metis: Racja, dzięki lim sinx/x= 1 x−>0