Pomoc przy zrozumieniu granic jednostronnych Hajcik: Czy ktoś mógłby mi pomóc przy zrozumieniu granic jednostronnych na konkretnych przykładach?

	x2
lim
	x2−1

x−> −1⁻

	x3 + 4x2 − 52
lim
	x3 + 8

x−> −2⁺ Wyznaczanie asymptot poziomych i pionowych na tym przykładzie?

	5x2 − 3x + 7
f(x) =
	3x2 + 8x

Oraz wyznaczenie granic jednostronnych funkcji f w punkcie x₀ lub w punktach x₁, x₂? { −1 dla x ≤ 2

	1
f(x) = {		x dla −2 < x < 2, x1 = −2, x2 = 2
	2

{1 dla x ≥ 2 Z góry dziękuję za pomoc!

Jerzy: 1) Jak x zmieraz do −1 z lewej strony , to po jakich wartościach ?

Hajcik: Po wartościach ujemnych, dążę od wartości ujemnych, tak?

Jerzy: Tzn ... po jakich wartościach mianownik zmierza do 0

Hajcik: W 1. chodzi tylko o obliczenie i są wyniki jedynie +∞ oraz −∞ w odpowiedziach. To jest przykład z Euklidesa dla kl.2 liceum zad 7.21.6.

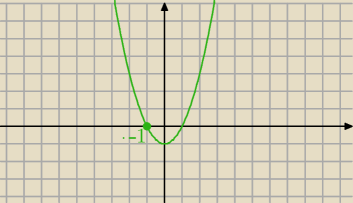
Jerzy: Tutaj masz wykres mianownika ..... i teraz się zastanów.

Hajcik: Po dodatnich, +∞ bo im większy mianownik tym szybciej zmierza do 0.

Jerzy: To widać na wykresie .... dla x < −1 mianownik jest dodatni , a więc zmierza do 0 po wartościach dodatnich , stąd lim = + ∞.

Hajcik: Nie do końca jestem pewny, ale które idą od +∞ do −1?

Jerzy: Jeśli x →−1⁺ , to mianownik zmierza do 0 po wartościach ujemnych , stąd lim = − ∞.

Hajcik: To wiele wyjaśnia, przy granicach które dążą do −∞ lub +∞ nie miałem problemów, jedynie na lekcji z wykorzystaniem definicji granicy w punkcie mnie nie było i stąd problem. Chociaź tyle wiem. Czyli w tego typu zadaniach trzeba zwracać w większej mierze uwagę na mianownik?

Jerzy: Patrz na wykres mianownika, dla x > −1 ( w pobliżu) mianownik jest ujemny.

Hajcik: A w drugim przykładzie? W mianowniku wychodzi ze wzoru skróconego mnożenia (x+2)(x² − 2x + 4) Δ<0, więc rozpatrywać powinienem deltę która jest pod osią OX i funkcję stałą = −2?