. Janek: Mógłby ktoś rzucić okiem i wskazać mi błąd bo wydaje mi sie ze zrobiłem to źle. Wyznacz równanie stycznej do wykresu w podanym punkcie f(x)= ln(x²+e) Punkt x0(0,f(0) ) robię to tak y−y0=f'(x0)(x−x0) y0=ln(0²+e)=ln e=1

	1		2x
f'(x)= ( ln(x2+e))'=		*(x2+e)'=
	x2+e		x2+e

	2*0		0
f(0)=		=		=0
	02+e		e

y−1=0(x−0) y=1 Z góry dzieki za pomoc.

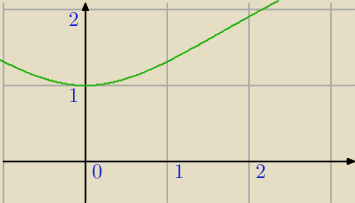
b.: Zgadza się, co można zobaczyć na rysunku, jak również z faktu, że f jest parzysta, więc styczna w zerze −− jeśli istnieje −− musi być pozioma.