help Agata: w czworokącie wypukłym suma długości przekątnych jest równa 20 cm , a kąt ostry między przekątnymi ma miarę 45 stopni. wyznacz długości przekątnych , dla których pole tego czworokąta jest największe z możliwych.

Agata: pomoże ktoś?

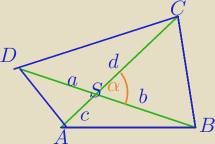
Mila: α=45^o AC=e, BD=f e+f=20 e=c+d, f=a+b

	1		1		1		1
P=		*d*b*sin45+		*a*c*sin45+		*c*bsin135+		*a*dsin135
	2		2		2		2

	√2		√2		√2
P=		*(bd+ac+bc+ad)=		*[a(c+d)+b*(d+c)]=		*(d+c)*(a+b)
	4		4		4

	√2		√2
P(e)=		*e*(20−e)=		*(20e−e2) parabola skierowana w dół.
	4		4

	−20
ew=		=10
	2*(−1)

e=10 i f=10

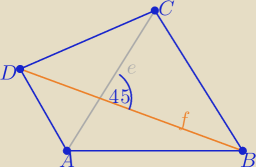Eta: Z treści zadania : f+e=20 ⇒ f=20−e , e∊(0,20)

	1		√2
P(ABCD)=		e*f*sin45o ⇒ P=		e*f
	2		4

	√2		√2
P(e)=		e(20−e) = −		e2+5e√2 −− parabola ramionami do dołu
	4		4

	−5√2
emax=		= 10 to fmax=20−10= 10
	−√2   2

e=10 i f=10 ===========