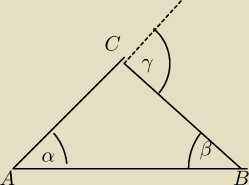
Rozdzial 3 5-latek: Ostatnie zadanie na dzisiaj zktorym sobie nie poradze . W trojkacie ABC kąt zewnetrzny przy wierzcholku C jest 5 razy wiekszy od kąta wewnwtrznego A i o 22^o wiekszy od kata wewnetrzenego B Oblicz kąty tego trojkata Wiem tyle γ kat zewznetrzny kąta C α i β kąty wewnwtrzentrzne nieprzylegle do kata γ i γ= α+β.

5-latek: napisze odp . 22^o, 70^o i 88^o

b.: układ równań: γ= α+β. γ = 5α γ = β + 22 kąty trójkąta (w stopniach) to α, β, 180 − γ

Mila: Myślałam, że obliczyłeś. ∡C=δ γ=5α γ=β+22 −−−−−−−−−−⇔5α=β+22 α+β+δ=180 γ+δ=180 −−−−−−− odejmuję stronami α+β−γ=0⇔α+β−5α=0 β=4α⇔ 4α=5α−22 α=22 β=88 δ=180−(22+88)=70

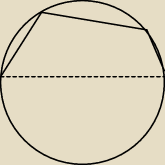
jc: Mam zadanie, z którym nie potrafię sobie poradzić. Dane są trzy odcinki. Jak dobrać okrąg, aby można było ułożyć je tak, jak na rysunku. Linia przerywana, to średnica.

5-latek: Milu Obliczylem tylko przeliczylem sie z silami dajac tak pozno zadanie Witaj jc

b.: 00:25: −− propozycja: skorzystać z tw, sinusów 549, skąd a = 2Rsin(α) b = 2Rsin(β) c = 2Rsin(γ) oraz (*) α + β + γ = π/2 (α = kąt wpisany oparty na odcinku długości a, itd.) Z (*) mamy sin(γ) = cos(α+β) = cos α cos β − sin α sin β, mnożąc obustronnie przez 4R² i korzystając z jedynki trygonometrycznej dostałem 2Rc = √4R²−a² √4R²−b² − ab, po napisaniu dwóch symetrycznych wersji i przekształceniach dostałem (ale mogłem się pomylić): abc + R(a²+b²+c²) = 4R³ i to jest warunek na R. (Teoretycznie można to równanie rozwiązywać...).

jc: b, bardzo dziękuję . Sprawdziłem. Jest OK. Zadanie wynikło z następującego problemu: Jak zbudować (płaski) parasol o największym polu dysponując drutami o długościach a,b,c. Wydaje mi się, że te dwa problemy są równoważne.