pochodna funkcji wykładniczej kondzik: Czy pochodna funkcji f(x)=(2x+1)e^−x wynosi (−2x+1)e^−x?

helps: 2e^−x−(2x+1)e^−x

helps: =e^−x(−2x+3)

helps: wydaje mi się raczej tak

Janek191: 23.07 źle

helps: sorry

kondzik: Możesz przedstawić swoje obliczenia? Ja licząc z pochodnej iloczynu otrzymałem f'(x)=2e^−x+(−2x−1)e^−x

Jerzy: 23:06...dobrze.

kondzik: Czyli zgadza się?

Jerzy: Tak.

kondzik: Pytam, bo badam przebieg zmienności funkcji i po przyrównaniu pochodnej do zera wyszło mi x=1/2, które jest jednocześnie maksimum lokalnym, więc f_max=f(1/2)=2e^−1/2. Jak mam to potem zaznaczyć na wykresie?

kondzik: Up

Adam: Liczysz pochodną f(x). Przyrównujesz ją do 0. Otrzymujesz punkt na osi x. Najlepiej jakbyś pokazał nam całość swoich obliczeń.

kondzik: f'(x)=(−2x+1)e^−x co zostało już wyżej sprawdzone (−2x+1)e^−x=0 −2x+1=0 x=1/2− maksimum lokalne f(max)=f(1/2)=2e^−1/2 Po prostu zastanawiam się czy wszystko jest dobrze,bo tą wartość maksymalną ciężko później zaznaczyć na wykresie

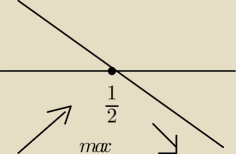
KKrzysiek: y(max)=2e^−1/2

KKrzysiek:

	1
F. osiąga maks. lokalne w punkcie (		,2e−1/2)
	2