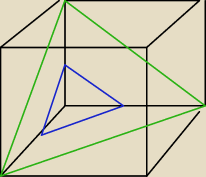
Sześcian o krawedzi a przecięto równoległymi płaszczyznami Pierwsza płaszczyzna zawiera srodki
krawedzi wychodzacych z jednego wierzchołka a druga przekatne trzech scian majacych wspolny
wierzchołek. Oblicz objetość każdej z trzech powstalych bryl
te trojkaty to trojkaty rownoboczne, wiec spodek wysokosci znajduje sie w 2/3 wysokosci tak?
wychodzą mi złe wyniki, mógłby ktos policzyc objetosc jednej z tej bryl bo moze cos zle robie
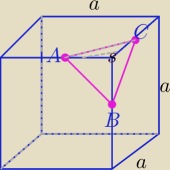Narysunku masz zaznaczone naroże sześcianu, po odcięciu jest
to ostrosłup prawidłowy trójkątny, wszystkie ściany boczne są trójkątami prostokątnymi.
Każdą ściankę możesz uznać za podstawę.
ΔABS− podstawa
| 1 | ||
V= | *PΔABS*|SC| | |
| 3 |
| 1 | 1 | a | a | a | a3 | |||||||
V= | *( | *( | * | )* | = | |||||||
| 3 | 2 | 2 | 2 | 2 | 48 |
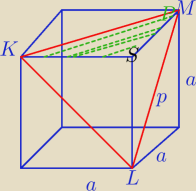Objętość ostrosłupa KLMS jest 23 razy większa od objętości ostrosłup poprzedniego
| a3 | a3 | |||
VKLMS=8* | = | |||
| 48 | 6 |
| 1 | ||
V= | *ΔKMS*|LS| | |
| 3 |
| 1 | 1 | a3 | ||||
V= | *( | *a*a)*a= | ||||
| 3 | 2 | 6 |